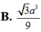Cho hình chóp S . A B C D có đáy ABCD là tứ giác lồi và góc tạo bởi các mặt phẳng ( S A B ) , ( S B C ) , ( S C D ) , ( S D A ) với mặt đáy lần lượt là 90 ° , 60 ° , 60 ° , 60 ° . Biết rằng tam giác SAB vuông cân tại S , A B = a và chu vi tứ giác ABCD là 9a. Tính thể tích V của khối chóp S . A B C D ?
A. V = a 3 3 4
B. V = a 3 3
C. V = 2 a 3 3 9
D. V = a 3 3 9
Đáp án D.
Gọi H là trung điểm của AB thì S H ⊥ A B C D ⇒ S H = a 2 .
Khoảng cách từ H đến BC, CD, DA đều là a 2 3 ⇒ S A B C D = 1 2 . a 2 3 . 9 a − a = 2 a 2 3 .
Vậy thể tích khối chóp S.ABCD là V S . A B C D = 1 3 S H . S A B C D = 1 3 . a 2 . 2 a 2 3 = a 3 3 9 .