Đáp án C.
Gọi G là trọng tâm Δ A B C ⇒ S G ⊥ ( A B C ) , I là trung điểm AB
A G = 2 3 . a 3 2 = a 3 3 ⇒ S G = S A 2 − A G 2 = a
I G = 1 3 C I = a 3 6
C G = a 3 3
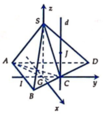
Chọn hệ trục tọa độ như hình vẽ: Ox qua G và song song AB
⇒ G 0 ; 0 ; 0 , S 0 ; 0 ; a , C 0 ; a 3 3 ; 0 ; B a 2 ; a 3 6 ; 0
C A = C B = C D ⇒ C là tâm đường tròn ngoại tiếp Δ A B D
Gọi d là đường thẳng qua C 0 ; a 3 3 ; 0 và vuông góc với (ABD)
⇒ V T P T k → = 0 ; 0 ; 1 ⇒ d : x = 0 y = a 3 3 z = t
Gọi tâm mặt cầu ngoại tiếp SABD là J ∈ d ⇒ J 0 ; a 3 3 ; t
Mà J S = J B ⇔ 0 2 + − a 3 3 2 + a − t 2 = a 2 2 + − a 3 6 − a 3 3 2 + t 2 ⇔ t = 1 6 a
⇒ R = 0 2 + a 3 3 2 + a − 1 6 a 2 = a 37 6

