\(\overrightarrow{AO}-\overrightarrow{OB}=\overrightarrow{AO}-\overrightarrow{DO}=\overrightarrow{AO}+\overrightarrow{OD}=\overrightarrow{AD}\)
Cho hình bình hành ABCD có tâm O. Chứng minh rằng:
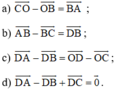
Cho hình bình hành ABCD tâm O. Chứng minh OA+OB+OC+OD= véctơ 0
Cho hình bình hành ABCD tâm O. Khi đó O B → - O A → bằng
A. O C → + O B →
B. B A →
C. O C → + O D →
D. C D →
Cho O là tâm hình bình hành ABCD. Hỏi vectơ A O → - D O → bằng vectơ nào?
Cho O là tâm hình bình hành ABCD. Hỏi vectơ ( A O → - D O → ) bằng vectơ nào?
a) Cho tứ giác ABCD không phải là hình bình hành, AC cắt BD tại O có OB = OD. Gọi M, N lần lượt là trung điểm của AB và CD, MN cắt AC tại I. Chứng minh rằng \(\overrightarrow{MI}=\overrightarrow{IN}\)
b) Cho tứ giác ABCD có 2 đường chéo cắt nhau tại I. Biết \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\). Chứng minh rằng tứ giác ABCD là hình bình hành
Trong mặt phẳng oxy, cho A(-1;5); B(1;-2); C(3;6) a) Chứng minh rằng A, B, C lập thành một tam giác. b) Tính tọa độ trọng tâm tam giác ABC. c) Tìm tọa độ điểm D của hình bình hành ABCD và tính tọa độ tâm của hình bình hành
Cho hình bình hành ABCD có tâm O. CMR
a/ vecto AB+OD+OC=AC
b/ vecto BA+BC+OB=OD
c/ vecto BA+BC=MO-MB-OB
1)Cho hình bình hành ABCD, xác định các vectơ DA+DC,AB+DA.
2)Cho 5 điểm A, B, C, D, E. Chứng minh rằng: AC-ED+CD+EC-BC = AB
3)Cho hình vuông ABCD, tâm O cạnh bằng a.
a) Xác định vecto BA+DA+AC, AB+CA+BC, AB+AC.
b) Tính độ dài vecto DA+DC, AB-BC
