Cho hình bình hành ABCD có B A D ^ < 90 ∘ . Giả sử O là điểm nằm trong Δ A B D sao cho OC không vuông góc với BD.
Vẽ đường tròn tâm O đi qua C.BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D.
Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q
2) CM cắt QN tại K, CN cắt PM tại L. Chứng minh rằng K L ⊥ O C .
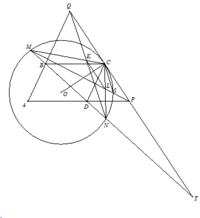
Gọi MP giao (O) tại điểm thứ hai S
Ta có các biến đổi góc sau:
K M L ^ = C M S ^ = S C P ^ (góc tạo bởi tiếp tuyến và dây cung)
= M S C ^ − S P C ^ (góc ngoài)
= M N C ^ − M N Q ^ (do các tứ giác MNPQ và MNSC nội tiếp).
= K N L ^
Từ đó tứ giác MKLN nội tiếp, suy ra K L M ^ = K N M ^ = Q P M ^ ⇒ K L ∥ P Q ⊥ O C
Vậy K L ⊥ O C .


