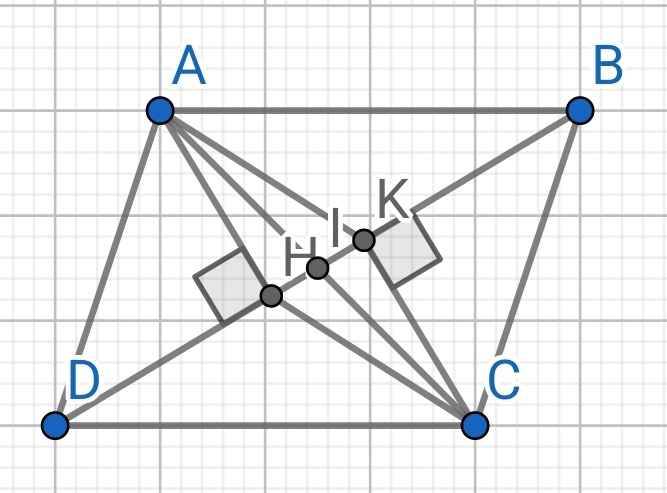
 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AD // BC
⇒ ∠ADH = ∠CBK (so le trong)
Do AH ⊥ BD (gt)
CK ⊥ BD (gt)
⇒ AH // CK
∆AHD và ∆CKB có:
AD = BC (hai cạnh đối của hình bình hành)
∠ADH = ∠CBK (cmt)
⇒ ∆AHD = ∆CKB (cạnh huyền - góc nhọn)
⇒ AH = CK (hai cạnh tương ứng)
Tứ giác AHCK có:
AH // CK (cmt)
AH = CK (hai cạnh tương ứng)
⇒ AHCK là hình bình hành
b) Do AHCK là hình bình hành (cmt)
I là trung điểm HK (gt)
⇒ I là trung điểm AC
Do ABCD là hình bình hành (gt)
I là trung điểm AC (cmt)
⇒ I là trung điểm BD
⇒ IB = ID
Đúng 6
Bình luận (0)

