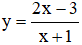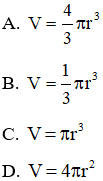Các câu hỏi tương tự
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho x=N.b, với a là hằng số, N là số nguyên dương
Tính : ax+20a(x-b)+21a(x-2b)+22a(x-3b)+23a(x-4b)+...+2N-2[x-(N-1)b]
Cho hàm số f(x) liên tục và a0. Giả sử với mọi
x
∈
0
;
a
ta có f(x)0 và f(x).f(a-x) 1. Tính
I
∫
0
a
d
x
1
+
f
(
x
)
Đọc tiếp
Cho hàm số f(x) liên tục và a>0. Giả sử với mọi x ∈ 0 ; a ta có f(x)>0 và f(x).f(a-x) = 1. Tính I = ∫ 0 a d x 1 + f ( x )
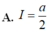
![]()
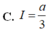
![]()
Cho số thực a0 Gỉa sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a-x) 1 Tính tích phân
I
∫
0
a
1
1
+
f
(
x
)
d
x
A. a/3 B. a/2 C. a D. 2a/3
Đọc tiếp
Cho số thực a>0 Gỉa sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a-x) = 1 Tính tích phân I = ∫ 0 a 1 1 + f ( x ) d x
A. a/3
B. a/2
C. a
D. 2a/3
Cho hàm số y f(x) liên tục trên R và a 0. Giả sử rằng với mọi
x
∈
0
;
a
, ta có f(x) 0 và f(x)f(a – x) 1. Tính
I
∫
0
a
d
x
1
+
f
(
x
)
. A.
a...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và a > 0. Giả sử rằng với mọi x ∈ 0 ; a , ta có f(x) > 0 và f(x)f(a – x) = 1. Tính I = ∫ 0 a d x 1 + f ( x ) .
A. a 2 .
B. 2a.
C. a 3 .
D. aln(a + 1).
Cho hàm số f(x)
ax
2
+
bx
+
1
,
x
≥
0
ax
-
b...
Đọc tiếp
Cho hàm số f(x)= ax 2 + bx + 1 , x ≥ 0 ax - b - 1 , x < 0
Khi hàm số f(x) có đạo hàm tại xo=0. Hãy tính T=a+2b.
A. T= -4
B. T=0
C. T= -6
D. T=4
Câu 1. Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số A. y -2 B. y -1 C. x 2 D. y 2Câu 2. Cho hàm số f(x) x2lnx. Tính f(e) A. 3e B. 2e C. e D. 2 + eCâu 3. Viết công thức tính V của khối cầu có bán kính r. Câu 4. Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng 6 gần bằng số nào sau đây nhất? A. 48 B. 46 C. 52 D. 51Câu 5. Tìm tập xác định D của hàm số y ln(x2 - 3x) A. D (0;3) B. D [0;3] C. D (-∞;0)∪(3;+∞) D. D (-∞;0)∪[3;+∞)
Đọc tiếp
Câu 1. Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số
A. y = -2
B. y = -1
C. x = 2
D. y = 2
Câu 2. Cho hàm số f(x) = x2lnx. Tính f'(e)
A. 3e
B. 2e
C. e
D. 2 + e
Câu 3. Viết công thức tính V của khối cầu có bán kính r.
Câu 4. Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng 6 gần bằng số nào sau đây nhất?
A. 48
B. 46
C. 52
D. 51
Câu 5. Tìm tập xác định D của hàm số y = ln(x2 - 3x)
A. D = (0;3)
B. D = [0;3]
C. D = (-∞;0)∪(3;+∞)
D. D = (-∞;0)∪[3;+∞)
Cho f(x) là hàm liên tục và a0. Giả sử rằng với mọi x thuộc [0;a] ta có f(x)0 và f(x).f(a-x) 1 Hãy tính
I
∫
0
a
d
x
1
+
f
(
x
)
theo a. A. a. B.
a
2
C. 2a D. 3a
Đọc tiếp
Cho f(x) là hàm liên tục và a>0. Giả sử rằng với mọi x thuộc [0;a] ta có f(x)>0 và f(x).f(a-x) = 1 Hãy tính I = ∫ 0 a d x 1 + f ( x ) theo a.
A. a.
B. a 2
C. 2a
D. 3a
Cho F'(x) = f(x), C là hằng số dương tùy ý.
Khi đó 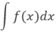 bằng:
bằng:
A. F(x) + C B. F(x) - C
C. F(x) + lnC D. F(x + C)