bằng:
Đáp án: C.
Vì lnC mới là số thực tùy ý, D sai vì không cộng hằng số C vào biến.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho F'(x) = f(x), C là hằng số dương tùy ý.
Khi đó ∫ f(x)dx bằng:
A. F(x) + C B. F(x) - C
C. F(x) + lnC D. F(x + C)
hàm số
f
(
x
)
ln
1
-
1
x
2
. Biết rằng
f
(
2
)
+
F
(
3
)
+
.
.
.
+
f
(
2018
)
ln
a
-
ln
b...
Đọc tiếp
hàm số f ( x ) = ln 1 - 1 x 2 . Biết rằng f ( 2 ) + F ( 3 ) + . . . + f ( 2018 ) = ln a - ln b + ln c - ln d với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và a<b<c<d. Tính P=a+b+c+d
A. 1986
B. 1698
C. 1689
D. 1968
H24
24 tháng 1 2022 lúc 22:03
Cho hàm số \(f\left(x\right)\) có đạo hàm bằng \(f'\left(x\right)=x^2\left(x-1\right)^3\left(x-2\right)\) . Số điểm cực trị của hàm số \(f\left(x\right)\) bằng:
A.0 B.1 C.2 D.3
Cho f(x) là hàm liên tục trên đoạn [0;a] thỏa mãn
f
(
x
)
.
f
(
a
-
x
)
1...
Đọc tiếp
Cho f(x) là hàm liên tục trên đoạn [0;a] thỏa mãn f ( x ) . f ( a - x ) = 1 f ( x ) > 0 ; ∀ x ∈ [ 0 ; a ] và ∫ 0 a d x 1 + f ( x ) = b a c , trong đó b, c là hai số nguyên dương và b/c là phân số tối giản. Khi đó b+c có giá trị thuộc khoảng nào dưới đây?
A. (11;22)
B. (0;9)
C. (7;21)
D. (2017;2020)
Cho
f
(
x
)
x
3
+
a
x
2
+
b
x
+
c
và
g
(
x
)
f
(
d
x
+
e
)
với
a
,
b
,
c
,
d
,
e
∈
ℝ
có đồ thị như hình v...
Đọc tiếp
Cho f ( x ) = x 3 + a x 2 + b x + c và g ( x ) = f ( d x + e ) với a , b , c , d , e ∈ ℝ có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x) Diện tích hình phẳng giới hạn bởi hai đường congy=f(x) và y=g(x) gần nhất với kết quả nào dưới đây?
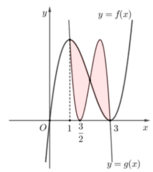
A. 4,5
B. 4,25
C. 3,63
D. 3,67
Cho các hàm số:
f
(
x
)
20
x
2
-
30
x
+
7
2
x
-
3
;
F
(
x
)
(
a
x
2
+
b...
Đọc tiếp
Cho các hàm số: f ( x ) = 20 x 2 - 30 x + 7 2 x - 3 ; F ( x ) = ( a x 2 + b x + C ) 2 x - 3 với x > 3 2 . Để F(x) là một nguyên hàm của f(x) thì giá trị của a,b,c lần lượt là:
A. a = 4; b = 2; c= 1
B. a = 4; b = -2; c = -1
C. a = 4; b = -2; c = 1
D. a = 4; b = 2; c = -1 .
Cho hàm số f(x) có đạo hàm f(x) liên tục trên R và có đồ thị của hàm số f(x) như hình vẽ, Biết
∫
0
3
(
x
+
1
)
f
(
x
)
d
x
a
và
∫
0
1
f
(
x...
Đọc tiếp
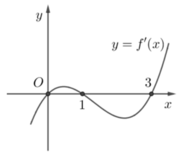
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên R và có đồ thị của hàm số f'(x) như hình vẽ, Biết ∫ 0 3 ( x + 1 ) f ' ( x ) d x = a
và ∫ 0 1 f ' ( x ) d x = b , ∫ 1 3 f ' ( x ) d x = c , f ( 1 ) = d Tích phân ∫ 0 3 f ( x ) d x bằng
A. -a+b+4c-5d
B. -a+b-3c+2d
C. -a+b-4c+3d
D. -a-b-4c+5d
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
m
,
a
,
b
,
c...
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + m , a , b , c , d , c , m ∈ ℝ . Hàm số y = f'(x) có đồ thị như hình vẽ bên.
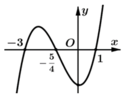
Tập nghiệm của phương trình f(x) = m có số phần tử là
A. 2.
B. 4.
C. 1.
D. 3.
Cho hàm số f(x) thỏa mãn f(x)f(x)1 với mọi x
∈
R. Biết
∫
1
2
f
(
x
)
d
x
a
và f(1)b, f(2)c Tích phân
∫
1
2
x
f
(
x
)
d
x
bằng
Đọc tiếp
Cho hàm số f(x) thỏa mãn f(x)f'(x)=1 với mọi
x ∈ R. Biết ∫ 1 2 f ( x ) d x = a và f(1)=b, f(2)=c Tích phân ∫ 1 2 x f ( x ) d x bằng
