Các câu hỏi tương tự
Cho hàm số y f(x) có đạo hàm liên tục trên R, đồ thị hàm y f’(x) như hình vẽ dưới đây. Khẳng định nào trong các phương án A, B, C, D dưới đây là đúng? A. . B. . C. . D. .
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R, đồ thị hàm y = f’(x) như hình vẽ dưới đây. Khẳng định nào trong các phương án A, B, C, D dưới đây là đúng?
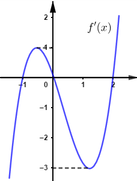
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f(x) liên tục trên (-∞;+∞) có BBT dưới đây. Tìm điều kiện của m để phương trình f(x)m có nghiệm.
Đọc tiếp
Cho hàm số f(x) liên tục trên (-∞;+∞) có BBT dưới đây. Tìm điều kiện của m để phương trình f(x)=m có nghiệm.
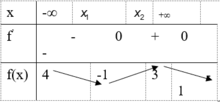
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có đạo hàm liên tục trên đoạn [-3;3] và đồ thị hàm số yf(x) như hình vẽ dưới đây Biết f(1)6 và g(x)f(x) -
x
+
1
2
2
. Mệnh đề nào sau đây là đúng? A. Phương trình g(x)0 có đúng hai nghiệm thuộc [-3;3]. B. Phương trình g(x)0 không có nghiệm thuộc [-3;3]. C. Phương trình g(x)0 có đúng một nghiệm thuộc [-3;3]. D. Phương t...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [-3;3] và đồ thị hàm số y=f'(x) như hình vẽ dưới đây
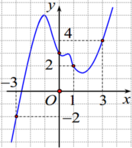
Biết f(1)=6 và g(x)=f(x) - x + 1 2 2 . Mệnh đề nào sau đây là đúng?
A. Phương trình g(x)=0 có đúng hai nghiệm thuộc [-3;3].
B. Phương trình g(x)=0 không có nghiệm thuộc [-3;3].
C. Phương trình g(x)=0 có đúng một nghiệm thuộc [-3;3].
D. Phương trình g(x)=0 có đúng ba nghiệm thuộc [-3;3].
Cho hàm số y f(x) có đạo hàm liên tục trên R Đồ thị hàm số y f’(x) như hình bên dưới Đặt g(x) f(x) - x khẳng định nào sau đây là đúng? A. g(2) g( -1) g(1) B. g( -1) g(1) g(2) C. g(-1) g( 1) g( 2) D. g( 1) g( -1) g( 2)
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm liên tục trên R Đồ thị hàm số y= f’(x) như hình bên dưới
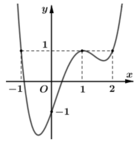
Đặt g(x) = f(x) - x khẳng định nào sau đây là đúng?
A. g(2) < g( -1) < g(1)
B. g( -1) < g(1) < g(2)
C. g(-1) > g( 1) > g( 2)
D. g( 1) < g( -1) < g( 2)
Hàm số y f(x) liên tục trên R và có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng? A. Hàm số có ba điểm cực trị B. Hàm số đạt cực đại tại x 0 C. Hàm số đạt cực tiểu tại x -1 D. Hàm số đạt cực đại tại x 2
Đọc tiếp
Hàm số y = f(x) liên tục trên R và có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng?
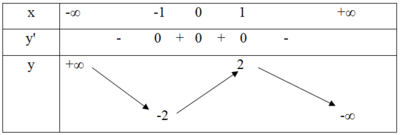
A. Hàm số có ba điểm cực trị
B. Hàm số đạt cực đại tại x = 0
C. Hàm số đạt cực tiểu tại x = -1
D. Hàm số đạt cực đại tại x = 2
Cho hàm số y f(x) liên tục trên [a;b] có đồ thị hàm số y f(x) như hình vẽ sau: Mệnh đề nào dưới đây đúng? A.
∫
a
b
f
(
x
)
d
x
là diện tích hình thang cong ABMN B.
∫
a
b
f
(
x
)
d
x
là độ dài đoạn BP. C....
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b] có đồ thị hàm số y = f'(x) như hình vẽ sau: Mệnh đề nào dưới đây đúng?
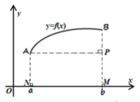
A. ∫ a b f ' ( x ) d x là diện tích hình thang cong ABMN
B. ∫ a b f ' ( x ) d x là độ dài đoạn BP.
C. ∫ a b f ' ( x ) d x là độ dài NM.
D. ∫ a b f ' ( x ) d x là độ dài đoạn cong AB
Cho hàm số yf(x) có đạo hàm và liên tục trên R. Biết rằng đồ thị hàm số yf (x) như hình dưới đây Lập hàm số g(x)f(x)-x^2-x. Mệnh đề nào sau đây đúng? A. B. C. D.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm và liên tục trên R. Biết rằng đồ thị hàm số y=f '(x) như hình dưới đây
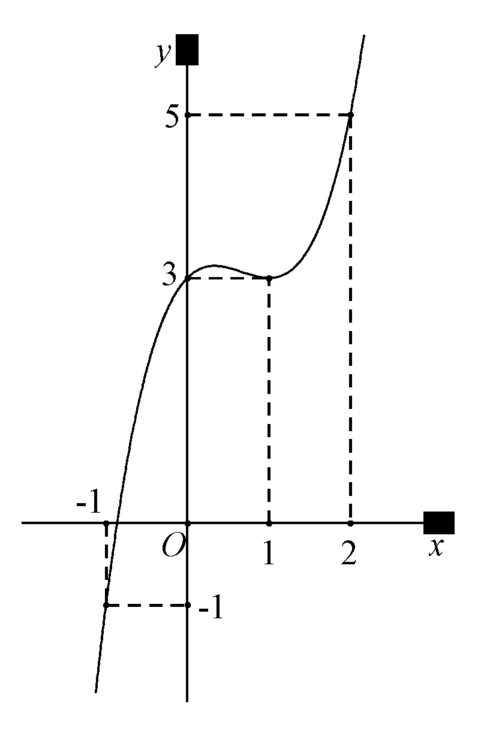
Lập hàm số g(x)=f(x)-x^2-x. Mệnh đề nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y f(x) có đạo hàm và liên tục trên R. Biết rằng đồ thị hàm số y f’(x) như hình dưới đây. Lập hàm số
g
(
x
)
f
(
x
)
-
x
2
-
x
. Mệnh đề nào sau đây đúng? A. . B. . C. . D. .
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm và liên tục trên R. Biết rằng đồ thị hàm số y = f’(x) như hình dưới đây.
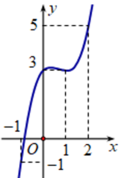
Lập hàm số g ( x ) = f ( x ) - x 2 - x . Mệnh đề nào sau đây đúng?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số yf(x) xác định, liên tục trên
ℝ
và có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng? A. Hàm số đồng biến trên khoảng
-
∞
;
1
B. Hàm số đồng biến trên khoảng
-
∞
;
-
1
C. Hàm số đồng biến tr...
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên ℝ và có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?
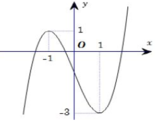
A. Hàm số đồng biến trên khoảng - ∞ ; 1
B. Hàm số đồng biến trên khoảng - ∞ ; - 1
C. Hàm số đồng biến trên khoảng 0 ; + ∞
D. Hàm số đồng biến trên khoảng - 3 ; + ∞

