Các câu hỏi tương tự
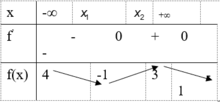
Cho hàm số f(x) liên tục trên R có bảng biến thiên dưới đây. Tìm điều kiện của m để phương trình |f(x)| m có 4 nghiệm phân biệt
Đọc tiếp
Cho hàm số f(x) liên tục trên R có bảng biến thiên dưới đây. Tìm điều kiện của m để phương trình |f(x)| = m có 4 nghiệm phân biệt
![]()
![]()
![]()
Cho hàm số f(x) liên tục trên
-
∞
;
+
∞
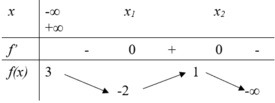
và có bảng biến thiên dưới đây. Tìm điều kiện của m để phương trình f(x)m có hai nghiệm phân biệt.
Đọc tiếp
Cho hàm số f(x) liên tục trên - ∞ ; + ∞ và có bảng biến thiên dưới đây. Tìm điều kiện của m để phương trình f(x)=m có hai nghiệm phân biệt.
![]()
![]()
![]()
![]()
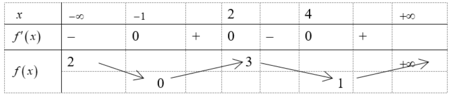
Cho hàm số yf(x) liên tục trên R có bảng biến thiên dưới đây. Tìm điều kiện của m để phương trình f(x)m có ba nghiệm phân biệt.
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R có bảng biến thiên dưới đây.
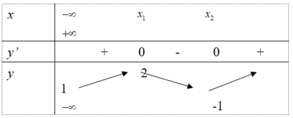
Tìm điều kiện của m để phương trình f(x)=m có ba nghiệm phân biệt.
![]()
![]()
![]()
![]()
Cho hàm số y f (x) liên tục trên R có bảng biến thiên dưới đây Tìm điều kiện để phương trình f(x)m có hai nghiệm phân biệt.
Đọc tiếp
Cho hàm số y = f (x) liên tục trên R có bảng biến thiên dưới đây
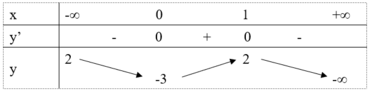
Tìm điều kiện để phương trình f(x)=m có hai nghiệm phân biệt.
![]()
![]()
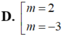
Cho hàm số f(x) liên tục trên có bảng biến thiên trên
-
1
;
2
như dưới đây. Tìm điều kiện m để phương trình có nghiệm
x
∈
-
1
;
2
.
Đọc tiếp
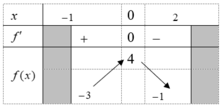
Cho hàm số f(x) liên tục trên có bảng biến thiên trên - 1 ; 2 như dưới đây. Tìm điều kiện m để phương trình có nghiệm x ∈ - 1 ; 2 .
![]()
![]()
![]()
![]()
Cho hàm số f(x) liên tục trên
-
∞
;
+
2
và
2
;
+
∞
có bảng biến thiên dưới đây. Tìm
m
∈
ℝ
để phương trình f(x) m có ba nghiệm phân biệt.
Đọc tiếp
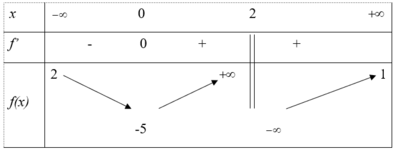
Cho hàm số f(x) liên tục trên - ∞ ; + 2 và 2 ; + ∞ có bảng biến thiên dưới đây. Tìm m ∈ ℝ để phương trình f(x) = m có ba nghiệm phân biệt.
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có đạo hàm liên tục trên R, đồ thị hàm số yf(x) như hình vẽ bên dưới. Cho bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
; với m là tham số thực. Tìm điều kiện cần và đủ để bất...
Đọc tiếp
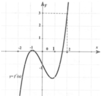
Cho hàm số y=f(x) có đạo hàm liên tục trên R, đồ thị hàm số y=f'(x) như hình vẽ bên dưới.
Cho bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
đúng với mọi
x
∈
-
2
;
2
![]()
![]()
![]()
![]()
![]()
Cho hàm số y f(x) xác định, liên tục trên
ℝ
{
1
}
và có bảng biến thiên dưới đây Tất cả các giá trị của m để phương trình f(x) m có ba nghiệm phân biệt là A. m
27
4
B. m 0 C. 0 m
27
4
D. m 0
Đọc tiếp
Cho hàm số y = f(x) xác định, liên tục trên ℝ \ { 1 } và có bảng biến thiên dưới đây
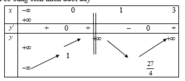
Tất cả các giá trị của m để phương trình f(x) = m có ba nghiệm phân biệt là
A. m > 27 4
B. m < 0
C. 0 < m < 27 4
D. m > 0
Cho hàm số y f (x) xác định, liên tục trên đoạn [-1;4]. Hàm số y f’(x) có đồ thị trên đoạn [-1;4] như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số thực m để bất phương trình
f
x
-
m
≥
0
nghiệm đúng với mọi x thuộc đoạn
3
2
;
10
3
A.
m
≤...
Đọc tiếp
Cho hàm số y = f (x) xác định, liên tục trên đoạn [-1;4]. Hàm số y = f’(x) có đồ thị trên đoạn [-1;4] như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số thực m để bất phương trình f x - m ≥ 0 nghiệm đúng với mọi x thuộc đoạn 3 2 ; 10 3
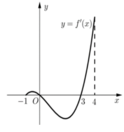
A. m ≤ f 3
B. m ≥ f 4
C. m ≤ f 3 2
D. m ≥ f 10 3