Các câu hỏi tương tự
Cho hàm số y=f(x) liên tục trên đoạn [-2;4] và có đồ thị như hình bên. Số nghiệm thực của phương trình 3f(x)-5=0 trên đoạn là
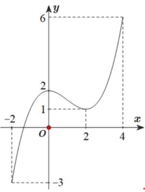
A. 1
B. 2
C. 3
D. 0
Cho hàm số yf(x) liên tục và có đồ thị trên đoạn [−2;4] như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số yf(x) trên đoạn [−2;4] bằng A. 5 B. 3 C. 0 D. -2
Đọc tiếp
Cho hàm số y=f(x) liên tục và có đồ thị trên đoạn [−2;4] như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số y=f(x) trên đoạn [−2;4] bằng
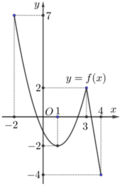
A. 5
B. 3
C. 0
D. -2
Cho hàm số y f(x) liên tục trên đoạn [1;3] và có bảng biến thiên như hình bên. Hỏi có tất cả bao nhiêu giá trị nguyên của m để phương trình
f
x
−
1
m
x
2
−
6
x
+
12
có hai nghiệm phân biệt trên đoạn [2;4]? A. 4. B. 5. C. 6. ...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [1;3] và có bảng biến thiên như hình bên. Hỏi có tất cả bao nhiêu giá trị nguyên của m để phương trình f x − 1 = m x 2 − 6 x + 12 có hai nghiệm phân biệt trên đoạn [2;4]?
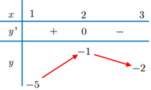
A. 4.
B. 5.
C. 6.
D. 7
Cho số thực m và hàm số yf(x) có đồ thị như hình vẽ. Phương trình
f
(
2
x
+
2
-
x
)
m
nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [-1;2]? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Cho số thực m và hàm số y=f(x) có đồ thị như hình vẽ. Phương trình f ( 2 x + 2 - x ) = m nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [-1;2]?

A. 2
B. 3
C. 4
D. 5
Cho số thực m và hàm số y f(x) có đồ thị như hình vẽ bên. Phương trình
f
2
x
+
2
-
x
có nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [-1;2]? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Cho số thực m và hàm số y = f(x) có đồ thị như hình vẽ bên. Phương trình f 2 x + 2 - x có nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [-1;2]?
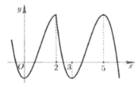
A. 2
B. 3
C. 4
D. 5
Cho hàm số yf(x) có đồ thị trên đoạn [-2;4] như hình vẽ. Tìm
max
max
−
2
;
4
f
x
A. 2 B.
f
0
C.3 D.1
Đọc tiếp
Cho hàm số y=f(x) có đồ thị trên đoạn [-2;4] như hình vẽ. Tìm max max − 2 ; 4 f x
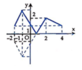
A. 2
B. f 0
C.3
D.1
Cho hàm số yf(x) liên tục trên R có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để phương trình f(f(x)-m)0 có tất cả 9 nghiệm thực phân biệt. A. 1. B. 0. C. 3. D. 2.
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để phương trình f(f(x)-m)=0 có tất cả 9 nghiệm thực phân biệt.
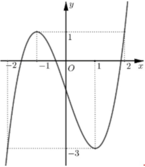
A. 1.
B. 0.
C. 3.
D. 2.
Cho hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
,
d
∈
R
có đồ thị như hình vẽ bên.Phương trình f(f(f(f(x))))0 có tất cả bao nhiêu nghiệm thực ph...
Đọc tiếp
Cho hàm số f x = a x 3 + b x 2 + c x + d a , b , c , d ∈ R có đồ thị như hình vẽ bên.
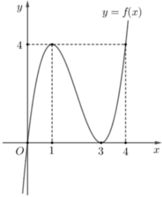
Phương trình f(f(f(f(x))))=0 có tất cả bao nhiêu nghiệm thực phân biệt?
A. 12
B. 40
C. 41
D. 16
Cho hàm số y f(x) liên tục và có đạo hàm trên
ℝ
, có đồ thị như hình vẽ bên. Với m là tham số thực bất kì thuộc đoạn [1;2]. Phương trình
f
x
3
−
3
x
2
m
3
−
3
m
2
+
5
có bao nhiêu nghiệm thực? A....
Đọc tiếp
Cho hàm số y = f(x) liên tục và có đạo hàm trên ℝ , có đồ thị như hình vẽ bên. Với m là tham số thực bất kì thuộc đoạn [1;2]. Phương trình f x 3 − 3 x 2 = m 3 − 3 m 2 + 5 có bao nhiêu nghiệm thực?
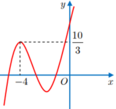
A. 3
B. 7
C. 5
D. 9



