Tiệm cận ngang y = 2 => a/1 = 2 => a = 2
Cắt trục tung tại y = 1 => b/1 = 1 => b = 1
Vậy chọn C. ab>0
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Cho
a
0
,
b
0
,
a
≠
1
,
b
≠
1
. Đồ thị hàm số
y
a
x
và
y
log
b
x
được xác định như hình vẽ bên. Mệnh đề nào sau đây là đúng? A.
a
1
;
0...
Đọc tiếp
Cho a > 0 , b > 0 , a ≠ 1 , b ≠ 1 . Đồ thị hàm số y = a x và y = log b x được xác định như hình vẽ bên. Mệnh đề nào sau đây là đúng?
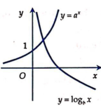
A. a > 1 ; 0 < b < 1.
B. 0 < a < 1 ; b > 1.
C. 0 < a < 1 ; 0 < b < 1.
D. a > 1 ; b > 1.
Cho a 0, b 0,
b
≠
1
Đồ thị các hàm số
y
a
x
và
y
log
b
x
cho như hình vẽ bên. Mệnh đề nào sau đây là đúng? A. a 1, 0 b 1 B. 1 a 0, b 1 C. 0 a 1, 0 b 1 D. a 1, b 1
Đọc tiếp
Cho a > 0, b > 0, b ≠ 1 Đồ thị các hàm số y = a x và y = log b x cho như hình vẽ bên. Mệnh đề nào sau đây là đúng?
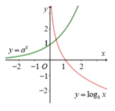
A. a > 1, 0 < b < 1
B. 1 > a > 0, b > 1
C. 0 < a < 1, 0 < b < 1
D. a > 1, b > 1
Hàm số
y
a
x
0
a
1
có đồ thị (C). Mệnh đề nào sau đây sai? A. Đồ thị (C) có tiệm cận y 0. B. Đồ thị (C) luôn nằm phía trên trục hoành C. Đồ thị (C) luôn đi qua
M
0
;
1
. D. Hàm số luôn đồng biến trên R.
Đọc tiếp
Hàm số y = a x 0 < a < 1 có đồ thị (C). Mệnh đề nào sau đây sai?
A. Đồ thị (C) có tiệm cận y = 0.
B. Đồ thị (C) luôn nằm phía trên trục hoành
C. Đồ thị (C) luôn đi qua M 0 ; 1 .
D. Hàm số luôn đồng biến trên R.
Hàm số
y
a
x
(
0
a
1
)
có đồ thị (C) Mệnh đề nào sau đây sai? A. Đồ thị (C) có tiệm cận y0 B. Đồ thị (C) luôn nằm phía trên trục hoành C. Đồ thị (C) luôn đi qua M(0;1) D. Hàm số luôn đồng biến trên R
Đọc tiếp
Hàm số y = a x ( 0 < a < 1 ) có đồ thị (C) Mệnh đề nào sau đây sai?
A. Đồ thị (C) có tiệm cận y=0
B. Đồ thị (C) luôn nằm phía trên trục hoành
C. Đồ thị (C) luôn đi qua M(0;1)
D. Hàm số luôn đồng biến trên R
Đồ thị hàm số y f(x) đối xứng với đồ thị của hàm số
y
a
x
(
a
0
,
a
≠
1
)
qua điểm I(1;1). Giá trị của biểu thức
2
+
log
a
1
2018
bằng
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị của hàm số y = a x ( a > 0 , a ≠ 1 ) qua điểm I(1;1). Giá trị của biểu thức 2 + log a 1 2018 bằng
Cho 3 số a, b, c 0,
a
≠
1
;
b
≠
1
;
c
≠
1
. Đồ thị các hàm số
y
a
x
,
y
b
x
,
y
c
x
được cho trong hình vẽ bên dưới. Mệnh đề nào sau đây đúng?
Đọc tiếp
Cho 3 số a, b, c > 0, a ≠ 1 ; b ≠ 1 ; c ≠ 1 . Đồ thị các hàm số y = a x , y = b x , y = c x được cho trong hình vẽ bên dưới. Mệnh đề nào sau đây đúng?
Cho hàm số yf(x) có đồ thị như sau. Số nghiệm thực của phương trình
f
2
(
x
)
-
1
0
là A. 7 B. 4 C. 3 D. 8
Đọc tiếp
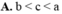
Cho hàm số y=f(x) có đồ thị như sau.
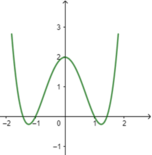
Số nghiệm thực của phương trình f 2 ( x ) - 1 = 0 là
A. 7
B. 4
C. 3
D. 8
Cho hàm số y f(x)
a
x
+
b
c
x
+
d
( a,b,c,d
∈
ℝ
,
-
d
c
≠
0) đồ thị hàm số y f’(x) như hình vẽ. Biết đồ thị hàm số y f(x) cắt...
Đọc tiếp
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.
Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Cho hàm số
y
a
x
+
b
c
x
+
d
a
≠
0
có đồ thị như hình bên dưới. A. Hàm số
y
a
x
3
+
b
x
2...
Đọc tiếp
Cho hàm số y = a x + b c x + d a ≠ 0 có đồ thị như hình bên dưới.
A. Hàm số y = a x 3 + b x 2 + c x + d có hai điểm cực trị trái dấu.
B. Đồ thị hàm số y = a x 3 + b x 2 + c x + d cắt trục tung tại điểm có tung độ dương
C. Đồ thị hàm số y = a x 3 + b x 2 + c x + d có hai điểm cực trị nằm bên phải trục tung
D. Tâm đối xứng của đồ thị hàm số y = a x 3 + b x 2 + c x + d nằm ở bên trái trục tung
DW
4 tháng 8 2021 lúc 16:55
Cho hàm số \(y=\dfrac{1}{2}x^4-x^2+m\)(m là tham số ) có đồ thị (Cm), đường tròn (S)có phương trình \(x^2+y^2+2x+6y+1=0\) và điểm A(-1;-6).Tìm m để tồn tại tiếp tuyến với đồ thị (Cm) cắt đường tròn (S) tại hai điểm phân biệt B,C sao cho tam giác ABC có chu vi đạt giá trị lớn nhất