Đồ thị hàm số đi qua A(1; 2) và B(-2; -1)
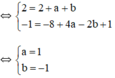
Đồ thị hàm số đi qua A(1; 2) và B(-2; -1)
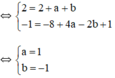
Xác định a, b, c, d để đồ thị của các hàm số:
y = x 2 + ax + b
và y = cx + d
cùng đi qua hai điểm M(1; 1) và B(3; 3).
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()
Cho hàm số y = x3 + ax2 + bx + c đi qua điểm A(0;-4) và đạt cực đại tại điểm B(1;0) hệ số góc k của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng -1 là:
A. k = 0
B. k = 24
C. k = -18
D. k = 18
Trong mặt phẳng tọa độ Oxy, cho đồ thị hàm số y = x + 1 x - 1 . A và B là hai điểm thay đổi trên đồ thị sao cho tiếp tuyến của đồ thị tại A và B song song với nhau. Biết rằng đường thẳng AB luôn đi qua một điểm cố định. Tọa độ của điểm đó là
![]()
![]()
![]()
![]()
Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường tròn C 1 và C 2 lần lượt có phương trình x - 1 2 + y - 2 2 = 1 và x + 1 2 + y 2 = 1 . Biết đồ thị hàm số y = a x + b x + c đi qua tâm của C 1 , đi qua tâm của C 2 và có các đường tiệm cận tiếp xúc với cả C 1 và C 2 . Tổng a+b+c là
A. 8
B. 2
C. -1
D. 5
Cho hàm số: y = f(x) = x 4 – 2m x 2 + m 3 – m 2
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 1.
b) Xác định m để đồ thị ( C m ) của hàm số đã cho tiếp xúc với trục hoành tại hai điểm phân biệt.
Cho hàm số có đồ thị (C) y = 2 x + 1 x - 1 và đường thẳng d: y=x+m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là
A.m=1
B.m=1 hoặc m=5
C.m=5
D.m=-5
Cho hai hàm số f ( x ) = x 4 - m - 1 x 2 + 2 và g ( x ) = 2 x 4 - 4 x 2 + 3 m . Giả sử đồ thị hàm số f(x) có ba điểm cực trị là A, B, C và đồ thị hàm số g(x) có ba điểm cực trị là M, N, P. Có bao nhiêu giá trị của tham số m để hai tam giác ABC và MNP đồng dạng với nhau?
A. 1.
B. 0.
C. 2.
D. 3.
Biết đồ thị hàm số y = x 3 + a x 2 + b x + c (với a, b, c là các số thực đi qua điểm (1;0) và có điểm cực trị (-2; 0)). Tính giá trị biểu thức T = a 2 + b 2 + c 2 + 2 .
A. 18
B. 7
C. 9
D. 27