Đáp án C.
Ta có y ' = 3 x 2 - 12 x + 9 .
Gọi M x 0 ; y 0 là tiếp điểm của tiếp tuyến đi qua A của đồ thị hàm số.
Lúc này tiếp tuyến có phương trình
y = 3 x o 2 - 12 x 0 + 9 x - x 0 + x 0 3 - 6 x 0 2 + 9 x 0 - 1
Tiếp tuyến đi qua A 1 ; m ⇒ m = 3 x 0 2 - 12 x 0 + 9 1 - x 0 + x 0 3 - 6 x 0 2 + 9 x 0 - 1
⇔ m = - 2 x 0 3 + 9 x 0 2 - 12 x 0 + 8 (*).
Để có đúng một tiếp tuyến của đồ thị hàm số đi qua A thì phương trình (*) có duy nhất một nghiệm.
Xét hàm số f ( x ) = - 2 x 0 3 + 9 x 0 2 - 12 x 0 + 8 có bảng biến thiên
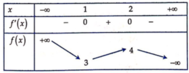
Để phương trình (*) có nghiệm duy nhất thì m > 4 m < 3 ⇔ m ∈ - ∞ ; 3 ∪ 4 ; + ∞ .
Vậy ta chọn C.

