Các câu hỏi tương tự
Cho hàm số
y
f
(
x
)
ax
3
+
bx
2
+
cx
+
d
có hai cực trị
x
1
,
x
2
thỏa
-
2
x
1
0
x
2
2...
Đọc tiếp
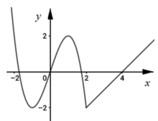
Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có hai cực trị x 1 , x 2 thỏa - 2 < x 1 < 0 < x 2 < 2 và có đồ thị như hình vẽ.
Số điểm cực tiểu của hàm số ![]() là
là
A. 3.
B. 5.
C. 7.
D. 4.
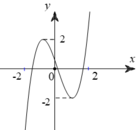
Cho hàm số y f(x) có đạo hàm và đồ thị hàm số y f’(x) như hình vẽ. Số điểm cực tiểu của hàm số là A.1 B . 2 C. 3 D. 4
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm ![]() và đồ thị hàm số y= f’(x) như hình vẽ.
và đồ thị hàm số y= f’(x) như hình vẽ.
Số điểm cực tiểu của hàm số ![]() là
là
A.1
B . 2
C. 3
D. 4
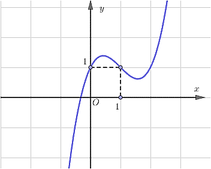
Cho hàm số y=f(x) có đồ thị như hình vẽ.
Điểm cực tiểu của hàm số là
A. x=0
B. y=0
C. y=-2
D. x=-2
Cho hàm số
y
a
x
4
+
b
x
3
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
;
a...
Đọc tiếp
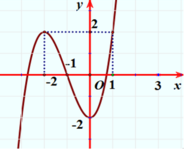
Cho hàm số y = a x 4 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a # 0 có đồ thị như hình vẽ bên.
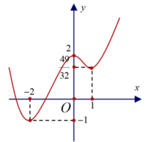
Các điểm cực tiểu của hàm số là
![]()
![]()
![]()
![]()
Cho hàm số y f(x) có đồ thị như hình vẽ bên dưới. Hàm số đã cho đạt cực tiểu tại điểm A. x -1 B. x1 C. x 0 D. x 2
Đọc tiếp
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.
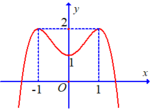
Hàm số đã cho đạt cực tiểu tại điểm
A. x= -1
B. x=1
C. x= 0
D. x= 2
Cho hàm số y = f ( x ) có đồ thị như hình vẽ bên dưới. Hàm số có bao nhiêu điểm cực tiểu trên khoảng a ; b ?
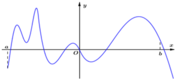
A. 4
B. 2
C. 7
D. 3
Cho hàm số y f (x) có đạo hàm trên
ℝ
. Biết hàm số
y
f
x
có đồ thị như hình vẽ. Hàm số g (x) f (x) + x đạt cực tiểu tại điểm A. x 1 B. x 2 C.Không có điểm cực tiểu D. x 0
Đọc tiếp
Cho hàm số y = f (x) có đạo hàm trên ℝ . Biết hàm số y = f ' x có đồ thị như hình vẽ. Hàm số g (x) = f (x) + x đạt cực tiểu tại điểm
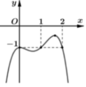
A. x = 1
B. x = 2
C.Không có điểm cực tiểu
D. x = 0
Cho hàm số
y
f
x
có đạo hàm trên
ℝ
. Đồ thị hàm số như hình vẽ bên dưới. Số điểm cực tiểu của hàm số
g
x
2
f
x
+
2
+
x
+
1
x
+
3
là
Đọc tiếp
Cho hàm số y = f x có đạo hàm trên ℝ . Đồ thị hàm số như hình vẽ bên dưới.
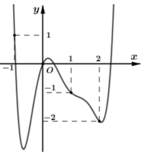
Số điểm cực tiểu của hàm số g x = 2 f x + 2 + x + 1 x + 3 là
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có bảng biến thiên như hình bên dưới. Phương trình đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số đã cho là
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình bên dưới.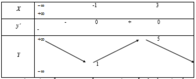
Phương trình đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số đã cho là
![]()
![]()
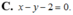
![]()