
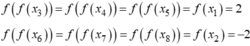
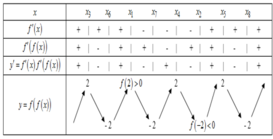
Suy ra số điểm cực tiểu của hàm số ![]() là 4
là 4

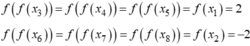

Suy ra số điểm cực tiểu của hàm số ![]() là 4
là 4
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:
I. Hàm số ![]() có 3 điểm cực trị.
có 3 điểm cực trị.
II. Hàm số g(x)đạt cực tiểu tại x=0
III. Hàm số g(x) đạt cực đại tại x=2
IV. Hàm số g(x) đồng biến trên khoảng (-2;0)
V. Hàm số g(x) nghịch biến trên khoảng (-1;1)
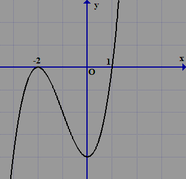
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.1
B.4
C.3
D.2
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị (C). Biết đồ thị hàm số (C) có hai điểm cực trị A(2;-27) ; B(-4;81). Tính S=-a+b-c+d
![]()
![]()
![]()
![]()
Cho hàm số bậc 4 y = f(x) có đồ thị như hình vẽ bên. Biết hàm số y = f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 = x1+2, f(x1) + f(x3) +\(\dfrac{2}{3}\)f(x2) = 0 và (C) nhận đường thẳng x = x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số \(\dfrac{S_1+S_2}{S_3+S_4}\) gần với kết quả nào nhất :
Cho hàm số y= f(x) có đạo hàm ![]() và đồ thị hàm số y= f’(x) như hình vẽ.
và đồ thị hàm số y= f’(x) như hình vẽ.
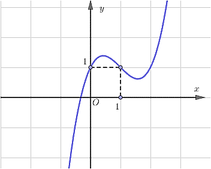
Số điểm cực tiểu của hàm số ![]() là
là
A.1
B . 2
C. 3
D. 4
chỉ mik cách lập nhóm nha
Trích một số bài toán trong đề:
+ Trên mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa mãn điều kiện /z/ = 2 là:
A. Đường tròn tâm O, bán kính R = 2
B. Đường tròn tâm O, bán kính R = 4
C. Đường tròn tâm O, bán kính R = 1/2
D. Đường tròn tâm O , bán kính R = căn 2
+ Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số y = f(x) có giá trị cực đại bằng 0
B. Giá trị lớn nhất của hàm số y = f(x) trên tập R là 1
C. Hàm số y = f(x) đạt cực đại tại x = 0 và cực tiểu tại x = -1
D. Hàm số y = f(x) có đúng một cực trị
+ Tìm phần thực của số phức (2 + 3i).i^10
Cho hàm số y = x 3 - 2 x 2 - 1 (1) và các mệnh đề
(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3
(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3
(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3
(4) Cực trị của hàm số (1) là x = 0 và x = 4/3
Trong các mệnh đề trên, số mệnh đề sai là:
A. 0
B. 1
C. 2
D. 3
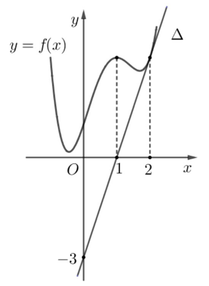
Cho hàm số f(x) có đạo hàm cấp hai f''(x) liên tục trên R và có đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x = 1 đường thẳng ![]() trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 . Tích phân
∫
0
ln
3
e
x
f
"
e
x
+
1
2
d
x
bằng
trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 . Tích phân
∫
0
ln
3
e
x
f
"
e
x
+
1
2
d
x
bằng
A. 8
B. 4
C. 3
D. 6