Đáp án C
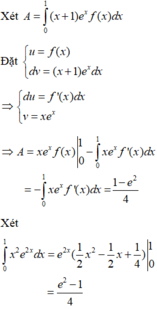
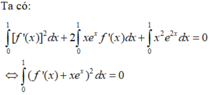
⇒ f ' ( x ) + x e x = 0 , ∀ x ∈ [ 0 ; 1 ] ( d o f ' x + x e x 2 ≥ 0 , ∀ x ∈ [ 0 ; 1 ] ) ⇒ f ' ( x ) = − x e x ⇒ f ( x ) = ( 1 − x ) e x + C f ( 1 ) = 0 ⇒ f ( x ) = ( 1 − x ) e x ⇒ I = ∫ 0 1 f ( x ) d x = ∫ 0 1 ( 1 − x ) e x d x = ( 2 − x ) e x 1 0 = e − 2

