Đáp án A
Gọi ![]() là điểm cố định cần tìm.
là điểm cố định cần tìm.
Ta có ![]()
![]() .
.
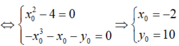
![]()
Lại có
![]()
Phương trình tiếp tuyến của ![]() có dạng
có dạng
![]() hay
hay
![]() .
.
Đường phân giác góc phần tư thứ nhất có phương trình d: y = x.
Vì
∆
vuông góc với d nên ta có ![]() .
.
Đáp án A
Gọi ![]() là điểm cố định cần tìm.
là điểm cố định cần tìm.
Ta có ![]()
![]() .
.
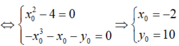
![]()
Lại có
![]()
Phương trình tiếp tuyến của ![]() có dạng
có dạng
![]() hay
hay
![]() .
.
Đường phân giác góc phần tư thứ nhất có phương trình d: y = x.
Vì
∆
vuông góc với d nên ta có ![]() .
.
Cho hàm số y = - x + 1 2 x - 1 có đồ thị là (C) , đường thẳng d: y=x+m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B. Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A; B . Tìm m để tổng k1+k2 đạt giá trị lớn nhất.
A. m=-1.
B.m=-2 .
C. m=3 .
D. m=-5.
Cho hàm số y = - x + 1 2 x - 1 có đồ thị là (C) , đường thẳng d: y= x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k1+ k2 đạt giá trị lớn nhất.
A. -2
B. -1
C. 1
D. 2
Cho hàm số y = 2 x - 1 x - 1 có đồ thị là (C) . Gọi I là giao điểm hai tiệm cận của (C) . tồn tại điểm M( a; b) với; a; b nguyên dương thuộc (C) có hoành độ lớn hơn 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng MI. Khi đó b-a= ?
A. 0
B. -1
C. 2
D. 1
Cho hàm số y = 2 x - 1 x + 1 có đồ thị (C) . Biết khoảng cách từ I(-1; 2) đến tiếp tuyến của (C) tại M là lớn nhất thì tung độ của điểm M nằm ở góc phần tư thứ hai, gần giá trị nào nhất?
A.3e
B.2e
C.e
D.4e
Cho hàm số y= x4- 2mx2+m (1) với m là tham số thực. Gọi (C) là đồ thị hàm số (1); d là tiếp tuyến của (C) tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm B( ¾; 1) đến đường thẳng d đạt giá trị lớn nhất?
A. 0
B. 1
C. 2
D. 3
Bài 1: Cho hàm số 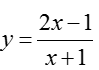
giúp mình bài này ik
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác ∆ O A B cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1.
D. -3.
Cho hàm số y = x 4 2 - 3 x 2 + 5 2 có đồ thị (C) và điểm M ∈ (C) có hoành độ x M = a. Có bao nhiêu giá trị nguyên của tham số a để tiếp tuyến của (C) tại M cắt (C) tại hai điểm phân biệt khác M.
A. 0.
B. 3.
C. 2.
D. 1.
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C) và điểm I (1; 2). Điểm M( a; b) ; a> 0 thuộc (C) sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM.
Giá trị a+ b bằng
A. 3
B . 4
C. 5
D. 6