+ Phương trình hoành độ giao điểm của d và (C) là
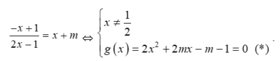
+ Theo định lí Viet ta có x1+ x2= -m ; x1.x2= ( -m-1) /2.
Gọi A( x1; y1) ; B( x2: y 2) .
+ Ta có y ' = - 1 ( 2 x - 1 ) 2 , nên tiếp tuyến của ( C) tại A và B có hệ số góc lần lượt là
k 1 = - 1 ( 2 x 1 - 1 ) 2 ; k 2 = - 1 ( 2 x 2 - 1 ) 2

Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng - 2 khi m= -1.
Chọn B.

