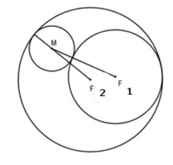
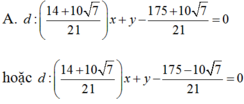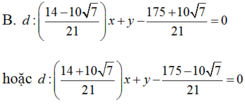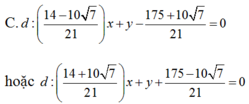Gọi C(M ; R).
C tiếp xúc ngoài với C1 ⇒ MF1 = R + R1
C tiếp xúc trong với C2 ⇒ MF2 = R2 – R
⇒ MF1 + MF2 = R + R1 + R2 – R = R1 + R2 = const.
Điểm M có tổng các khoảng cách MF1 + MF2 đến hai điểm cố định F1 và F2 bằng một độ dài không đổi R1 + R2.
Vậy M nằm trên elip có hai tiêu điểm F1, F2 và có độ dài trục lớn bằng R1 + R2.