Đáp án A.
Diện tích của (H) bằng S = ∫ 0 2 x d x + ∫ 2 4 x - x - 2 d x = 10 3 .
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Đáp án A.
Diện tích của (H) bằng S = ∫ 0 2 x d x + ∫ 2 4 x - x - 2 d x = 10 3 .
Cho (H) là hình phẳng giới hạn bởi y = x , y = x - 2 và trục hoành (hình vẽ).
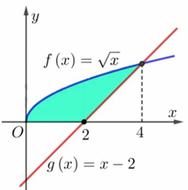
Diện tích của (H) bằng
A. 10 3
B. 16 3
C. 7 3
D. 8 3
Cho (H) là hình phẳng giới hạn bởi đường cong y = x , trục hoành và đường thẳng y=2-x (phần tô đậm trong hình vẽ bên). Diện tích của (H) bằng
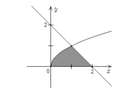
A. 4 2 - 1 3
B. 7 6
C. 8 2 + 3 6
D. 5 6
Gọi (H) là hình phẳng giới hạn bởi parabol (P): y = 8 x - x 2 và trục hoành. Các đường thẳng y=a,y=b,y=c với 0<a<b<c<16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức ( 16 - a ) 3 + ( 16 - b ) 3 + ( 16 - c ) 3 bằng
A. 2048.
B. 3584.
C. 2816.
D. 3480.
Cho (H) là hình phẳng giới hạn bởi parabol y = 1 4 x 2 + 1 với 0 ≤ x ≤ 2 2 , nửa đường tròn y = 8 - x 2 và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
A. 3 π + 14 6
B. 3 π + 2 3
C. 3 π + 4 3
D. c
Cho (H) là hình phẳng giới hạn bởi parabol y = 1 4 x 2 + 1 (với 0 ≤ x ≤ 2 2 ), nửa đường tròn y = 8 - x 2 và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
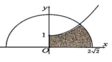
A. 3 π + 14 6
B. 2 π + 2 3
C. 3 π + 4 6
D. 3 π + 2 3
Gọi (H) là hình phẳng giới hạn bởi parabol y = ( x - 3 ) 2 trục hoành và trục tung. Gọi k 1 , k 2 k 1 , k 2 lần lượt là hệ số góc của đường thẳng qua điểm A(0;9) và chia (H) thành ba hình mặt phẳng có diện tích bằng nhau( tham khảo hình vẽ bên). Giá trị của k 1 - k 2 bằng
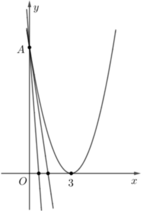
A. 13 2
B. 7
C. 25 4
D. 27 4
Cho (H) là hình phẳng giới hạn bởi parabol y = 2 x 2 4 đường cong y = 1 - x 2 4 (với 0 ≤ x ≤ 2 ) và trục hoành (tham khảo hình vẽ bên).
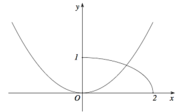
Diện tích của (H) bằng
A. 3 π - 2 12
B. 3 π + 4 2 - 6 12
C. 4 π + 3 2 - 8 12
D. π + 2 - 2 3
Cho (H) là hình phẳng giới hạn bởi parabol y = 2 x 2 4 , đường cong 1 - x 2 4 (với 0 ≤ x ≤ 2 ) và trục hoành (tham khảo hình vẽ bên). Diện tích của (H) bằng
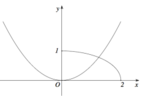
A. 3 π - 2 12
B. 3 π + 4 2 - 6 12
C. 4 π + 3 2 - 8 12
D. π + 2 - 2 3
Cho (H) là hình phẳng giới hạn bởi Parabol y = 3 x 2 , cung tròn có phương trình y = 4 − x 2 0 ≤ x ≤ 2 và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
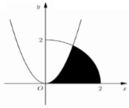
A. 4 π + 3 12 .
B. 4 π − 3 6 .
C. 4 π + 2 3 − 3 6 .
D. 5 3 − 2 π 3 .