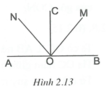
 a) Ta có
A
O
N
^
+
B
O
N
^
=
180
°
;
B
O
M
^
+
A
O
M
^
=
180
°
(hai góc kề bù) mà
A
O
M
^
=
B
O
N
^
(đề bài cho) nên
A
O
N
^
=
B
O
M
^
.
a) Ta có
A
O
N
^
+
B
O
N
^
=
180
°
;
B
O
M
^
+
A
O
M
^
=
180
°
(hai góc kề bù) mà
A
O
M
^
=
B
O
N
^
(đề bài cho) nên
A
O
N
^
=
B
O
M
^
.
Mặt khác, tia OC là tia phân giác của góc MON nên C O N ^ = C O M ^ .
Do đó A O N ^ + C O N ^ = B O M ^ + C O M ^ (1)
Ta có tia ON nằm giữa hai tia OA, OC; tia OM nằm giữa hai tia OB, OC nên từ (1) suy ra A O C ^ = B O C ^ = 180 ° : 2 = 90 ° . Vậy O C ⊥ A B .
b) Tia OM nằm giữa hai tia OB và ON nên B O M ^ + M O N ^ = B O N ^ = m ° (1).
Mặt khác B O M ^ = 180 ° − A O M ^ = 180 ° − m ° (2).
Từ (1) và (2) suy ra: 180 ° − m ° + 90 ° = m ° ⇒ 2 m ° = 270 ° ⇒ m ° = 135 ° .
Vậy m = 135 .
Chứng minh một tia là tia phân giác, là tia đối

