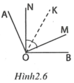
* Tìm cách giải
Để chứng tỏ O M ⊥ A B ta cần chứng tỏ góc AOM (hoặc góc BOM) có số đo bằng 90 ° .
* Trình bày lời giải
Ta có A O E ^ = B O F ^ ; M O E ^ = M O F ^ (đề bài cho)
⇒ A O E ^ + M O E ^ = B O F ^ + M O F ^ (1)
Tia OE nằm giữa hai tia OA, OM; tia OF nằm giữa hai tia OB, OM nên từ (1) suy ra A O M ^ = B O M ^ . Mặt khác, A O M ^ + B O M ^ = 180 ° (hai góc kề bù) nên A O M ^ = 180 ° : 2 = 90 ° , suy ra O M ⊥ O A . Do đó O M ⊥ A B

