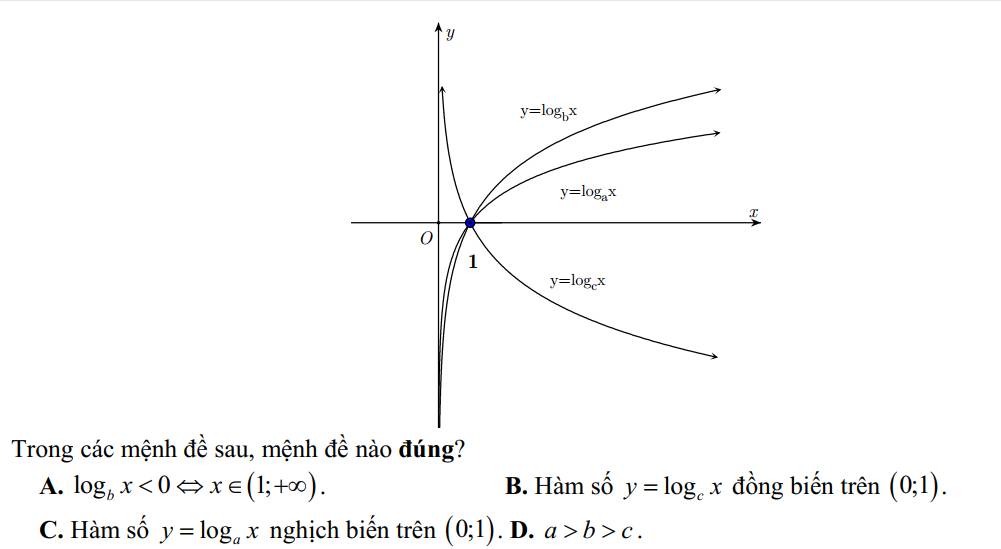
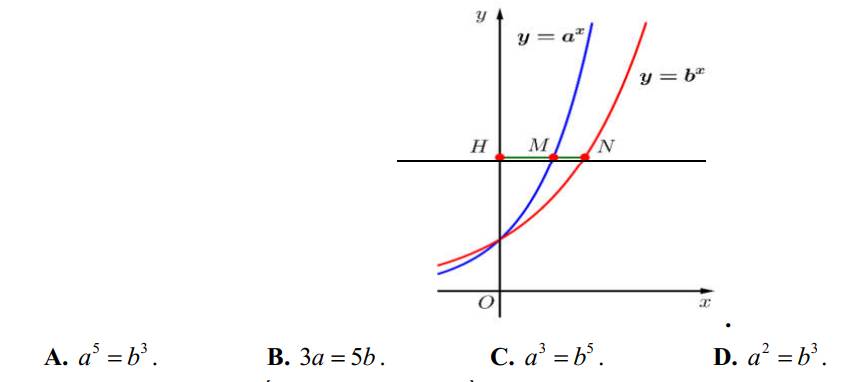
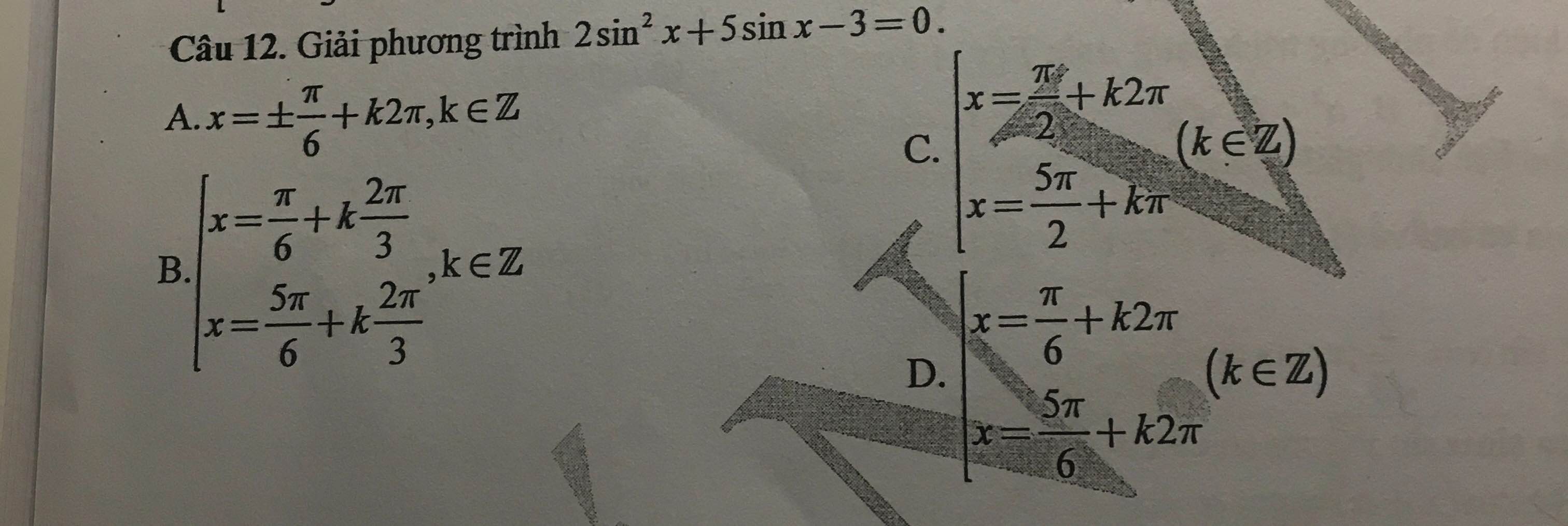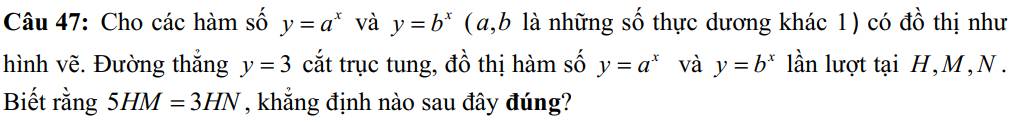Câu 1: D
Câu 2: A
Câu 3: D
Câu 4: C
Câu 5: \(u_5=u_2\cdot q^3\)
=>\(q^3=\dfrac{48}{-6}=-8=\left(-2\right)^3\)
=>q=-2
\(u_1=\dfrac{u_2}{q}=\dfrac{-6}{-2}=3\)
Tổng của 5 số hạng đầu là:
\(S_5=\dfrac{3\cdot\left(1-q^5\right)}{1-q}=\dfrac{3\cdot\left(1-\left(-2\right)^5\right)}{1-\left(-2\right)}=\dfrac{3\cdot\left(1+32\right)}{1+2}=1+32=33\)
=>Chọn C
Câu 6: B
Câu 7: A
Câu 8: \(sin\left(2x+\dfrac{\Omega}{3}\right)=\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}2x+\dfrac{\Omega}{3}=\dfrac{\Omega}{6}+k2\Omega\\2x+\dfrac{\Omega}{3}=\dfrac{5}{6}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2x=\dfrac{\Omega}{6}-\dfrac{\Omega}{3}+k2\Omega=-\dfrac{\Omega}{6}+k2\Omega\\2x=\dfrac{1}{2}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{\Omega}{12}+k\Omega\\x=\dfrac{1}{4}\Omega+k\Omega\end{matrix}\right.\)
=>Có 4 điểm biểu diễn
=>Chọn D
Câu 10: \(cosx\cdot sin\left(2x-\dfrac{\Omega}{3}\right)=0\)
=>\(\left[{}\begin{matrix}cosx=0\\sin\left(2x-\dfrac{\Omega}{3}\right)=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{2}+k\Omega\\2x-\dfrac{\Omega}{3}=k\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Omega}{2}+k\Omega\\2x=\dfrac{\Omega}{3}+k\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{2}+k\Omega\\x=\dfrac{\Omega}{6}+\dfrac{k\Omega}{2}\end{matrix}\right.\)
=>Chọn C