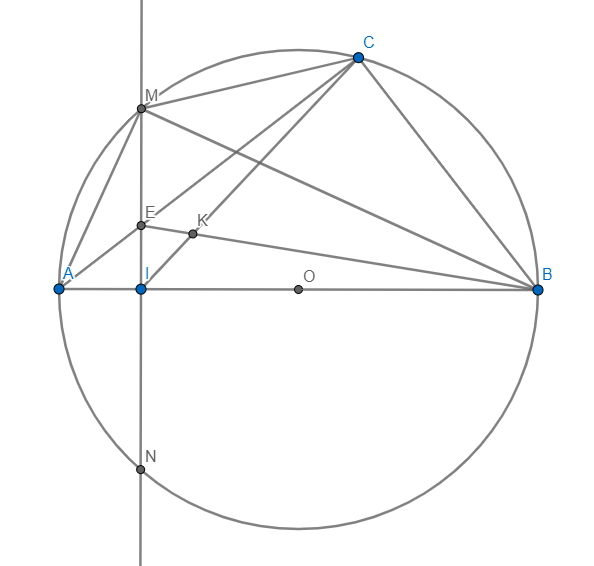
Cho đường tròn tâm O, đường kính AB cố định. Điểm I nằm giữa A và O. Kẻ dây MN LAB tại I. Gọi C là một điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và B. Nối AC, cắt MN tại E. Chứng minh rằng: 1) Tứ giác IECB nội tiếp được trong một đường tròn. 2) Tam giác AME đồng dạng với tam giác ACM. 3) IB.EK = EC.IK với K là giao điểm của CI và BE.
1) Vì AB là đường kính \(\Rightarrow\angle ACB=90\)
\(\Rightarrow\angle ECB+\angle EIB=90+90=180\Rightarrow IECB\) nội tiếp
2)Vì AB là đường kính \(\Rightarrow\angle AMB=90\)
Ta có: \(\angle AME=90-\angle MAB=\angle ABM=\angle ACM\) (ABCM nội tiếp)
Xét \(\Delta AME\) và \(\Delta ACM:\) Ta có: \(\left\{{}\begin{matrix}\angle AME=\angle ACM\\\angle CAMchung\end{matrix}\right.\)
\(\Rightarrow\Delta AME\sim\Delta ACM\left(g-g\right)\)
3) Vì IECB nội tiếp \(\Rightarrow\angle IBK=\angle ECK\)
Xét \(\Delta EKC\) và \(\Delta IKB:\) Ta có: \(\left\{{}\begin{matrix}\angle IKB=\angle EKC\\\angle IBK=\angle ECK\end{matrix}\right.\)
\(\Rightarrow\Delta EKC\sim\Delta IKB\left(g-g\right)\Rightarrow\dfrac{EK}{IK}=\dfrac{EC}{IB}\Rightarrow EK.IB=EC.IK\)