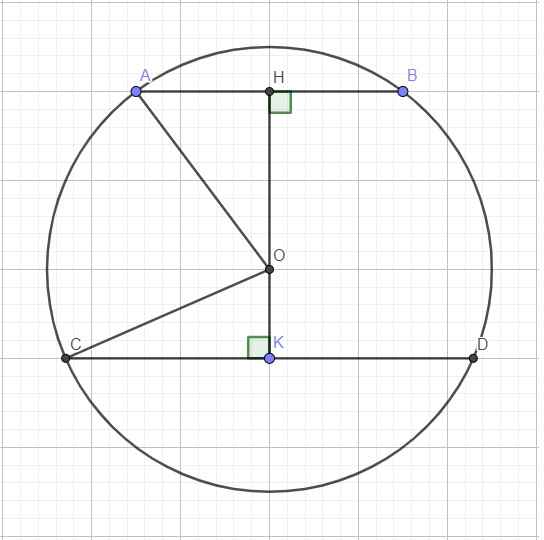
Từ O kẻ đường thẳng vuông góc AB và CD, cắt AB và CD lần lượt tại H và K
\(\Rightarrow\) H là trung điểm AB và K là trung điểm CD
\(\Rightarrow\left\{{}\begin{matrix}AH=\dfrac{1}{2}AB=4\\CK=\dfrac{1}{2}CD=4,8\end{matrix}\right.\)
Áp dụng định lý Pitago cho tam giác vuông OAH (với chú ý \(OA=OC=R=5\))
\(OH=\sqrt{OA^2-AH^2}=3\left(cm\right)\)
Pitago tam giác OCK:
\(OK=\sqrt{OC^2-CK^2}=1,4\left(cm\right)\)
\(\Rightarrow HK=OH+OK=4,4\left(cm\right)\)