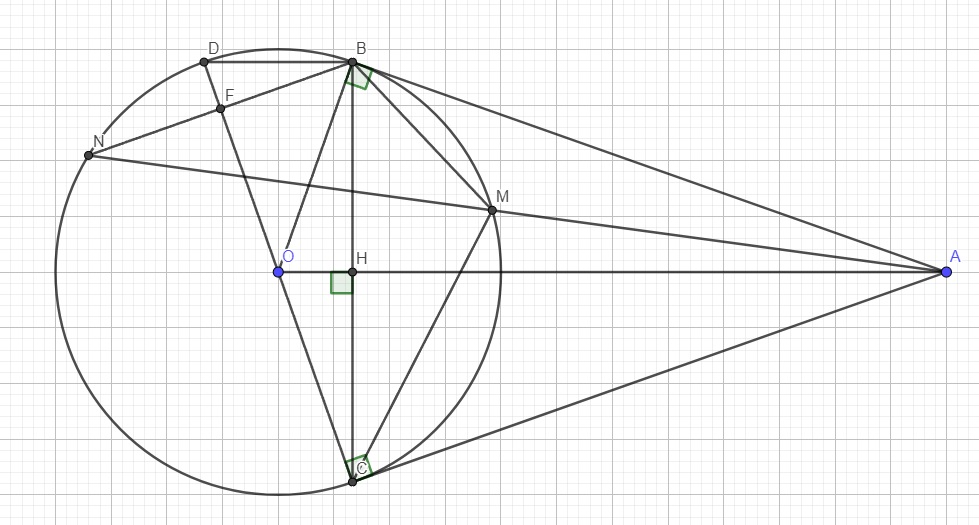
Cho đường tròn (O;R) và một điểm À nằm bên ngoài đường tròn với OA=3R.Qua À vẽ hai tiếp tuyến AB, AC để đường tròn (O) (B, C là hai tiếp điểm) a) Chứng minh tứ giác APOS nội tiếp b) Kẻ đường kính CD của (O). Chứng minhBD//OA. c) Kẻ dây BN của (O) song song với AC, AN cắt (O) ở M. Chứng minh MC²=MA.MB d) Gọi F là giao điểm của BN với CD. Tính the R diện tích của tam giác BCF
Câu a chắc em nhầm đề, ko có điểm S và P nào (chắc là ABOC) nhưng câu này đơn giản em có thể tự chứng minh
b.
Gọi H là giao điểm OA và BC
Ta có: \(AB=AC\) (t/c hai tiếp tuyến cắt nhau) và \(OB=OC=R\)
\(\Rightarrow OA\) là trung trực của BC \(\Rightarrow OA\perp BC\) tại H và H là trung điểm BC
Lại có CD là đường kính \(\Rightarrow\widehat{CBD}=90^0\) (góc nt chắn nửa đường tròn)
\(\Rightarrow BD\perp CD\)
\(\Rightarrow BD||OA\) (cùng vuông góc CD)
c.
Ta có BN song song AC \(\Rightarrow\widehat{BNM}=\widehat{MAC}\) (so le trong)
Mà \(\widehat{BNM}=\widehat{MCB}\) (cùng chắn BM)
\(\Rightarrow\widehat{MAC}=\widehat{MCB}\)
Xét hai tam giác MAC và MCB có:
\(\left\{{}\begin{matrix}\widehat{MAC}=\widehat{MCB}\left(cmt\right)\\\widehat{MCA}=\widehat{MBC}\left(\text{cùng chắn CM}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MAC\sim\Delta MCB\left(g.g\right)\)
\(\Rightarrow\dfrac{MC}{MB}=\dfrac{MA}{MC}\Rightarrow MC^2=MA.MB\)
d.
Do AC là tiếp tuyến \(\Rightarrow AC\perp OC\) hay \(AC\perp CF\)
Mà \(AC||BN\left(gt\right)\Rightarrow BN\perp CF\Rightarrow\Delta BCF\) vuông tại F
Xét hai tam giác COH và CBF có:
\(\left\{{}\begin{matrix}\widehat{HCO}-chung\\\widehat{COH}=\widehat{CBF}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta CBF\sim\Delta COH\) theo tỉ số đồng dạng \(k=\dfrac{BC}{OC}\)
\(\Rightarrow S_{BCF}=S_{COH}.k^2\)
Trong tam giác vuông OAB: \(cos\widehat{BOA}=\dfrac{OB}{OA}=\dfrac{R}{3R}=\dfrac{1}{3}\)
Trong tam giác vuông OBH: \(cos\widehat{BOH}=cos\widehat{BOA}=\dfrac{OH}{OB}\)
\(\Rightarrow OH=OB.cos\widehat{BOA}=R.\dfrac{1}{3}=\dfrac{R}{3}\)
\(\Rightarrow BH=\sqrt{OB^2-OH^2}=\sqrt{R^2-\left(\dfrac{R}{3}\right)^2}=\dfrac{2R\sqrt{2}}{3}=CH\)
\(\Rightarrow BC=2BH=\dfrac{4R\sqrt{2}}{3}\)
\(\Rightarrow S_{BCF}=\dfrac{1}{2}.OH.CH.\left(\dfrac{BC}{OC}\right)^2=\dfrac{1}{2}.\dfrac{R}{3}.\dfrac{2R\sqrt{2}}{3}.\left(\dfrac{\dfrac{4R\sqrt{2}}{3}}{R}\right)^2=\dfrac{32R^2\sqrt{2}}{81}\)