a: \(sđ\stackrel\frown{AnB}=\widehat{AOB}=60^0\)
b: Xét (O) có \(\widehat{ACB}\) là góc nội tiếp chắn cung AB
nên \(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{AOB}=30^0\)
c: Độ dài cung AnB là:
\(\dfrac{\Omega\cdot6\cdot60}{180}=2\Omega\)
a: \(sđ\stackrel\frown{AnB}=\widehat{AOB}=60^0\)
b: Xét (O) có \(\widehat{ACB}\) là góc nội tiếp chắn cung AB
nên \(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{AOB}=30^0\)
c: Độ dài cung AnB là:
\(\dfrac{\Omega\cdot6\cdot60}{180}=2\Omega\)
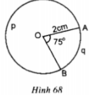
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc A O B = 75 °
a) Tính sđ góc ApB
b) Tính độ dài hai cung AqB và ApB
c) Tính diện tích hình quạt tròn OAqB
bài 1: cho đường tròn tâm /o bán kính 2cm. Góc SOB =60.
a) tính sđ cung AmB
b) tính độ dài hai cung AnB và AmB, độ dài đường tròn tâm O
c) tính diện tích hình tròn, diện tích hình quạt tròn OAnB.
bài 2: cho tam giác ABC có 3 góc nhọn. Đừng tròn tâm O đường kính BC cắt AB, AC lần lượt tại I và K. BK và CI cắt nhua tại H. Tia AH cắt BC tại M.
a) chứng minh \(AM\perp BC\)
b) chứng minh tứ giác BIHM, CMHK, AKMB nội tiếp. xác định tâm đường tròn ngoại tiếp
cho tam gíc ABC nội tiếp đường tròn (O) bán kính R có góc C = 45 độ
a. tính diện tích hình quạt tròn AOB (ứng với cung nhỏ AB)
b. tính diện tích hình viên phân AmB (ứng với cung nhỏ AB)
cho (O;3cm) lấy A,B trên (O) chia đường tròn thành 2 cung, cung nhỏ AmB và cung lớn AnB sao AOB =80°
a/tính số đo ANB
b/ tính độ dài cung AmB
c/ Tính diện tích, chu vi đường tròn (O)
d/ tính diện tích hình quạt tròn OAnB
Cho đường tròn tâm O, bán kính R=3 cm và hai điểm A,B nằm trên đường tròn (O) sao cho số đo cung lớn bằng 240°. Tính diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OB vsf cung nhỏ AB.
Cho đường tròn (O; 4cm) có đường kính BC. Gọi A là điểm nằm trên đường tròn sao cho góc vuông ABC=30°. Trên tia AC lấy điểm P sao cho AP=AB. Đường thẳng vuông góc hạ từ P xuống BC cắt BC ở H và cắt BA ở D. Kẻ PB cắt đường tròn (O) tại I.
a)Tính độ dài đường tròn và diện tích hình tròn.
b)Chứng minh tứ giác ACHD nội tiếp.
c)Tam giác ABP là tam giác gì? Tính góc vuông APB, sđ cung ACI.
d)Tính độ dài cung tròn cung ACI và diện diện của hình quạt OAI.
Cho đường tròn (O) đường kính AB. Lấy M thuộc đoạn AB. vẽ dây CD vuông góc với AB tại M. Giả sử AM = 2cm và CD = 4 3 cm. Tính:
a, Độ dài đường tròn (O) và diện tích đường tròn (O)
b, Độ dài cung C A D ⏜ và diện tích hình quạt tròn giói hạn bởi hai bán kính OC, OD và cung nhỏ C D ⏜
Bài tập 1:Cho đường tròn đồng tâm O, bán kính lần lượt R=5cm,r=2cm.lấy 2 điểm A,B thuộc (O;2) sao cho góc AOB=70 độ.Tia OA,OB cắt đường tròn (O;R) tại D và E, lấy điểm C thuộc đường tròn (O;r).
a) tính góc DOE, góc DCE.
b)Tính độ dài cung đường tròn (O;R) ;(O;r); độ dài cung tròn DE
c) Tính diện tích hình tròn (O;r) và hình quạt tròn DOE.(Lấy Pi=3,14).
Bài tập 2: Cho tam giác ABC nhọn,BC cố định.Kẻ đường cao AH và BK cắt nhau tại G.
a) Chứng minh tứ giác CHGK nội tiếp và tìm đường kính.
b)AH.BC=BK.AC
c)Vẽ đường tròn đường kính BC.Lấy điểm M thuộc đường tròn này.Tìm quỹ tích điểm N nằm trên tia BM sao cho MN=AC
ad và mọi người giải chi tiết và cho em hình minh họa luôn nhé ạ! Em cảm ơn nhiều ạ!
cho đường tròn tâm (O) bán kính 3cm trên (O) lấy điểm A,B sao cho góc AOB=60 độ. Tính số đo cung nhỏ AB,diện tích hình quạt tròn OAB,độ dài cung lớn AB
Cho tam giác ABC nội tếp đường tròn (O; 6cm). Tính diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OC và cung nhỏ AC khi A B C ^ = 60 0