Question

Cho đường tròn (O); đường kính AB. Kẻ tiếp tuyến tại B với đường tròn (O); trên tiếp tuyến này lấy điểm P. Qua A kẻ đường thẳng song song với OP cắt đường tròn (O) tại Q. Cm PQ là tiếp tuyến của đường tròn (O)

Answer 1

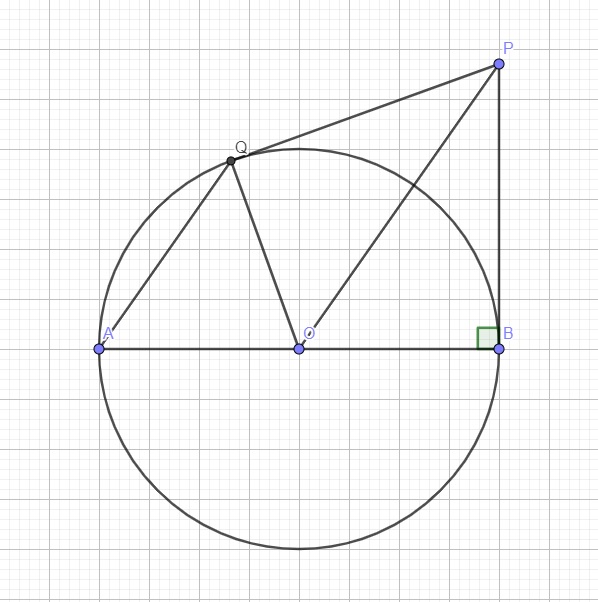
Do \(OA=OQ\) (cùng bằng bán kính đường tròn)

\(\Rightarrow\Delta OAQ\) cân tại O

\(\Rightarrow\widehat{AQO}=\widehat{QAO}\) (1)

Lại có \(AQ||OP\) theo giả thiết

\(\Rightarrow\left\{{}\begin{matrix}\widehat{AQO}=\widehat{QOP}\left(\text{so le trong}\right)\\\widehat{QAO}=\widehat{BOP}\left(\text{đồng vị}\right)\end{matrix}\right.\)   (2)

(1);(2) \(\Rightarrow\widehat{QOP}=\widehat{BOP}\)

Xét hai tam giác POQ và POB có: \(\left\{{}\begin{matrix}OQ=OB=R\\\widehat{QOP}=\widehat{BOP}\\OP\text{ chung}\end{matrix}\right.\)

\(\Rightarrow\Delta POQ=\Delta POB\left(c.g.c\right)\Rightarrow\widehat{PQO}=\widehat{PBO}=90^0\)

\(\Rightarrow PQ\perp OQ\Rightarrow PQ\) là tiếp tuyến của (O)

Answer 2