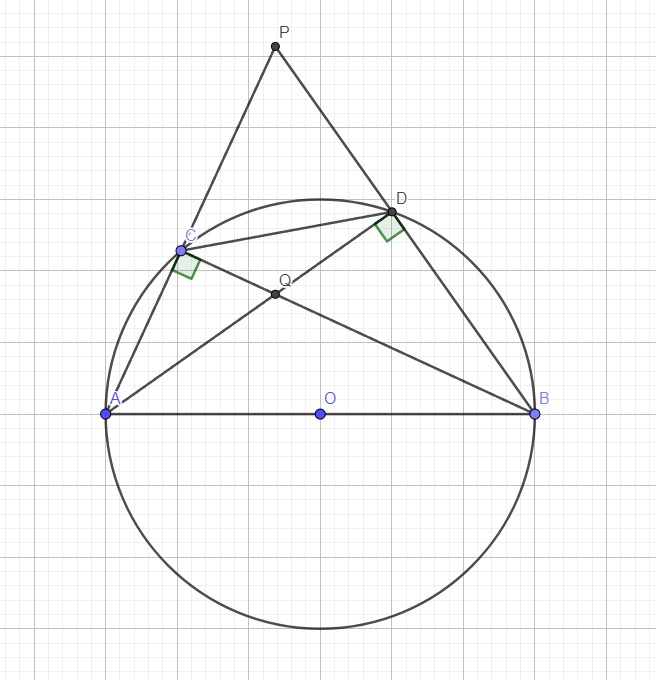
Do \(OC=OD=CD=R\Rightarrow\Delta OCD\) là tam giác đều
\(\Rightarrow\widehat{COD}=60^0\)
Mà \(\widehat{CAD}=\dfrac{1}{2}\widehat{COD}\) (góc nt và góc ở tâm cùng chắn CD)
\(\Rightarrow\widehat{CAD}=30^0\)
AB là đường kính nên \(\widehat{ADB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ADB}=90^0\)
\(\Rightarrow\widehat{ADP}=90^0\Rightarrow\widehat{APB}=180^0-\left(90^0+30^0\right)=60^0\)
Tương tự ta có \(\widehat{ACB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=90^0\Rightarrow\widehat{BCP}=90^0\)
\(\Rightarrow\widehat{CQD}=360^0-\left(\widehat{APB}+\widehat{ADP}+\widehat{ACB}\right)=360^0-\left(60^0+90^0+90^0\right)=120^0\)
\(\Rightarrow\widehat{AQB}=\widehat{CQD}=120^0\) (2 góc đối đỉnh)