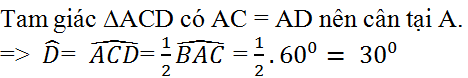Hướng dẫn làm bài:
Giả sử, gọi cạnh hình vuông là a và bán kính đường tròn là R.
Khi đó, chu vi hình vuông là 4a và chu vi hình tròn là 2πR.
Theo đề bài ra ta có: 4a=2πR⇒a=πR24a=2πR⇒a=πR2
Ta lập tỉ số diện tích hình vuông và hình tròn:
ShvShtr=a2πR2=(πR22)πR2=π2R24πR2=π4<1ShvShtr=a2πR2=(πR22)πR2=π2R24πR2=π4<1 (vì π ≈ 3,14)
⇒ Shv < Shtr
Vậy hình tròn có diện tích lớn hơn hình vuông
Hướng dẫn làm bài:
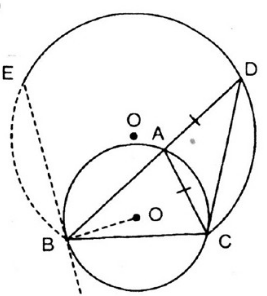
Ta có ˆA=12sđcungBC=600;ˆBDC=12.600=300A^=12sđcungBC=600;BDC^=12.600=300
Như vậy, điểm D tạo với hai mút của đoạn thẳng BC cố định một góc ˆBDC=300BDC^=300 nên D chuyển động trên cung chứa góc 30° dựng trên BC.
Ta có, khi A ≡ B thì D ≡ E và khi A ≡ C thì D ≡ C
Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chưa góc 30° dựng trên BC
Điểm D tạo với hai mút của đoạn thẳng BC cố định góc BDC bằng 30o nên D chuyển động trên cung chứa góc 30o dựng trên BC.
Khi A ≡ C thì D≡ C, khi A≡ B thì D≡ P(BP là tiếp tuyến của đường tròn (O) tại B).
Vậy khi A di chuyển trên cung lớn BC, D di chuyển trên cung CP thuộc cung chứa góc 30odựng trên BC.