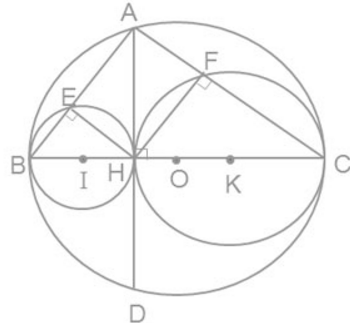
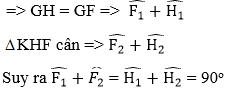Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF
a) Hãy xác định vị trí tương đối của các đường tròn : (I) và (O), (K) và (O), (I) và (K)
b) Tứ giác AEHF là hình gì ? Vì sao ?
c) Chứng minh đẳng thức AE.AB = AF.AC
d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K)
e) Xác định vị trí của điểm H để EF có độ dài lớn nhất
a) Hình bên
IA = OB – IB => (I) tiếp xúc trong với (O).
OK = OC – KC => (K) tiếp xúc trong với (O)
IK = OH + KH => (I) tiếp xúc ngoài với (K)
Chú ý: Từ các tam giác nội tiếp đường tròn ABC, BEH, CEH ta rút ra nhận xét sau: "Nếu tam giác nội tiếp đường tròn có một cạnh là đường kính thì tam giác đó là tam giác vuông".
c) AHB vuông nên AE.AB = AH2, AHC vuông nên AF.AC = AH2
Suy ra AE.AB = AF.AC
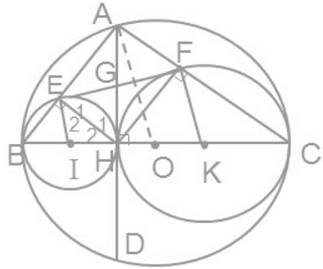
d) Gọi G là giao điểm của AH và EF
Do đó EF là tiếp tuyến của đường tròn (K)
Tương tự, EF là tiếp tuyến của đường tròn (I)
e) Hình bên
Cách 1: EF = AH ≤ OA (OA có độ dài không đổi)
EF = OA <=> AH = OA <=> H trùng O <=> dây AD đi qua O.
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.
Cách 2: EF = AH = AD/2.
Do đó: EF lớn nhất <=> AD lớn nhất <=> dây AD là đường kính.
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.
a) Hình bên
IA = OB – IB => (I) tiếp xúc trong với (O).
OK = OC – KC => (K) tiếp xúc trong với (O)
IK = OH + KH => (I) tiếp xúc ngoài với (K)
Chú ý: Từ các tam giác nội tiếp đường tròn ABC, BEH, CEH ta rút ra nhận xét sau: "Nếu tam giác nội tiếp đường tròn có một cạnh là đường kính thì tam giác đó là tam giác vuông".
c) AHB vuông nên AE.AB = AH2, AHC vuông nên AF.AC = AH2
Suy ra AE.AB = AF.AC
d) Gọi G là giao điểm của AH và EF
Do đó EF là tiếp tuyến của đường tròn (K)
Tương tự, EF là tiếp tuyến của đường tròn (I)
e) Hình bên
Cách 1: EF = AH ≤ OA (OA có độ dài không đổi)
EF = OA <=> AH = OA <=> H trùng O <=> dây AD đi qua O.
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.
Cách 2: EF = AH = AD/2.
Do đó: EF lớn nhất <=> AD lớn nhất <=> dây AD là đường kính.
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.