Chọn đáp án D
Vì hai đường tròn có một điểm chung là A và 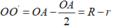 nên hai đường tròn tiếp xúc trong
nên hai đường tròn tiếp xúc trong
Chọn đáp án D

Vì hai đường tròn có một điểm chung là A và 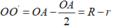 nên hai đường tròn tiếp xúc trong
nên hai đường tròn tiếp xúc trong
Cho hai đường tròn ( O ) và ( O' ) tiếp xúc ngoài ở A . Tiếp tuyến chung ngoài của 2 đường tròn , tiếp xúc với ( O ) ở M , tiếp xúc với đường tròn ( O' ) ở N . Qua A kẻ đường thẳng vuông góc với OO' cắt MN ở I .
a) CM : tam giác AMN vuông
b) Tam giác IOO' là tam giác gì ? Vì sao
c) CMR : đường thẳng MN tiếp xúc với đường tròn đường kính OO'
d) Cho biết OA = 8cm , OA' = 4,5 cm . TÍnh độ dài MN .
Hai đường tròn (O ; R) và (O' ; r) tiếp xúc ngoài với nhau. Gọi AB là tiếp tuyến chung của hai đường tròn, A∈(O),B∈(O′).
a) Tính độ dài AB.
b) Cho R=36cm,r=9cm. Tính bán kính của đường tròn (I) tiếp xúc với đường thẳng AB và tiếp xúc ngoài với hai đường tròn (O) và (O').
Cho(O;R) và điểm A nằm ngoài(O). Vẽ đường tròn đường kính OA, đường tròn này cắt (O) tại B và C. Vẽ BI là đường kính của đường tròn đường kính OA, vẽ BK là đường kính của (O).c/m
a) AB, AC là hai tiếp tuyến của (O)
b) IK là tiếp tuyến của (B;BC)
Cho đường tròn (O) và đường tròn (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài của cả 2 đường tròn (B, C là các tiếp điểm). tiếp tuyến chung trong của 2 đường tròn tại A cắt BC tại M a) CMR: A, , C thuộc đường tròn (M) đường kính BC b) Đường thẳng OO’ có vị trí như thế nào đối với đường tròn (M; BC/2) c) Xác định tâm của đường tròn đi qua O, M, O’ d) CMR: BC là tiếp tuyến của đường tròn đi qua O, M, O’.
cho hai đường tròn (o;r) và đường tròn (o'r) tiếp xúc ngoài vs nhau tại A, kẻ tiếp tuyến Ax. Kẻ đường thẳng tiếp xúc vs đường tròn (O) tại B và đt (O') tại C (B,C khác A). BC cắt Ax tại H. Kẻ đường kính BD của đt (O) và đường kính CE của đt (O'). Gọi I là trung điểm của DE.Cm: BC là tiếp tuyến của đường tròn ngoại tiếp \(\Delta\)OIO'
Cho nửa đường tròn (O;R), đường kính AB. Vẽ các tiếp tuyến Ax và By với nửa đường tròn. Các đường tròn (I) và (K) tiếp xúc ngoài với nhau và tiếp xúc ngoài với nửa đường tròn, trong đó đường tròn (I) tiếp xúc với Ax tại C, đường tròn (K) tiếp xúc với By tại D. Gọi a,b lần lượt là bán kính của (I) và (K). Chứng minh rằng \(R=2\sqrt{ab}\)
cho đường thẳng OO' và điểm A nằm giữa 2 điểm O và O' vẽ đường tròn tâm O bán kính OA và tâm O' bán kính O'A qua A vẽ đường thẳng cắt đường tròn O tại B và O' tại C.
a,CMR: O và ' tiếp xúc nhau
b, vẽ đường kính BD của đường tròn O và CE của O'. CMR: D,A,E thange hảng
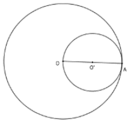
Cho đường tròn (O) bán kính OA và đường tròn (O') đường kính OA. Vị trí tương đối của hai đường tròn là:
A. Nằm ngoài nhau
B. Không giao nhau
C. Cắt nhau
D. Tiếp xúc
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O’). Đường tròn đường kính OC cắt (O) tại M và N. a/ Đường thẳng CM cắt (O’) tại P. Chứng minh: OM//BP. b/ Từ C kẻ đường thẳng vuông góc với CM cắt tia ON tại D. Chứng minh: Tam giác OCD là tam giác cân.