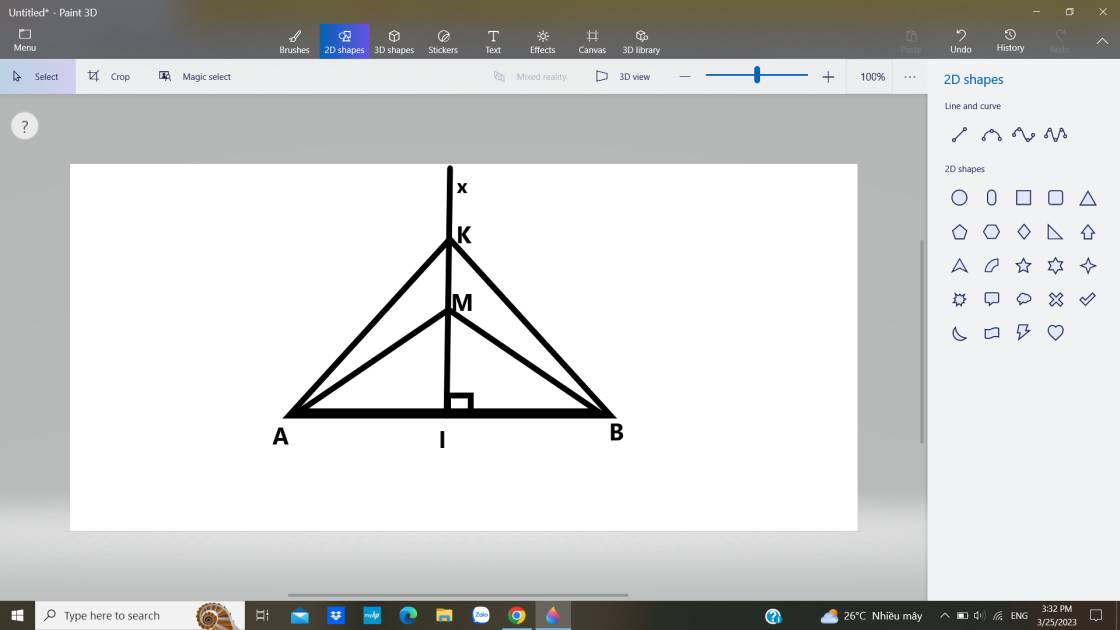
a) Do IM vuông góc với AB tại I và I là trung điểm AB
⇒ IM là đường trung trực của AB
⇒ MA = MB (tính chất đường trung trực của đoạn thẳng)
⇒ ∆MAB cân tại M
b) Do KM ⊥ AB (Ix ⊥ AB)
⇒ ∆KIA vuông tại I
Mà IK = IA (gt)
⇒ ∆KIA vuông cân tại I
⇒ ∠IKA = ∠IAK = 90⁰ : 2 = 45⁰
∆KIB vuông tại I
Mà IK = IB (gt)
⇒ ∆KIB vuông cân tại I
⇒ ∠IKB = ∠IBK = 90⁰ : 2 = 45⁰
⇒ ∠KAB = ∠KBA = 45⁰
⇒ ∆KAB cân tại K (1)
∆KAB có:
∠AKB + ∠KAB + ∠KBA = 180⁰
⇒ ∠AKB = 180⁰ - (∠KAB + ∠KBA)
= 180⁰ - (45⁰ + 45⁰)
= 90⁰
⇒ ∆KAB vuông tại K (2)
Từ (1) và (2) ⇒ ∆KAB vuông cân tại K