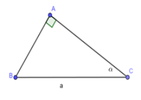
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
=>DE/BC=AD/AB=cosA
=>DE=BC*cosA
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp đường tròn đường kính BC
=>M là tâm đường tròn ngoại tiếp tứ giác BEDC
ΔMDE đều khi MD=ME=DE
=>MD=BC*cosA
mà MD=BC/2
nên BC/2=BC*cosA
=>BC*cosA-BC/2=0
=>\(BC\cdot\left(cosA-\dfrac{1}{2}\right)=0\)
=>\(cosA=\dfrac{1}{2}\)
=>\(\widehat{A}=60^0\)