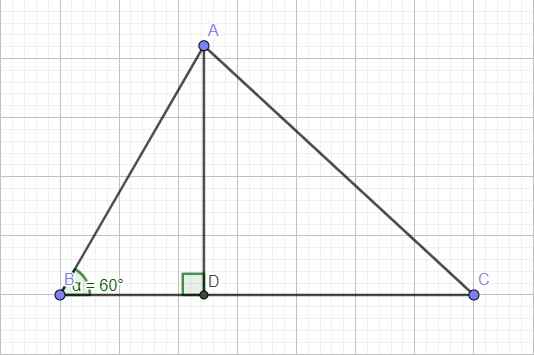
Kẻ đường cao AD, đặt \(AB=x>0\) ; \(BD=y>0\)
\(\Rightarrow AC=12-x\) ; \(CD=8-y\)
Trong tam giác vuông ABD:
\(BD=AB.cosB\Leftrightarrow y=x.cos60^0=\dfrac{x}{2}\) \(\Rightarrow CD=8-\dfrac{x}{2}\)
Theo định lý Pitago:
\(\left\{{}\begin{matrix}AD^2=AB^2-BD^2\\AD^2=AC^2-CD^2\end{matrix}\right.\) \(\Rightarrow AB^2-BD^2=AC^2-CD^2\)
\(\Leftrightarrow x^2-\left(\dfrac{x}{2}\right)^2=\left(12-x\right)^2-\left(8-\dfrac{x}{2}\right)^2\)
\(\Leftrightarrow16x-80=0\)
\(\Rightarrow x=5\)
Vậy \(\left\{{}\begin{matrix}AB=5\\AC=7\end{matrix}\right.\)