Xét ΔBAC có
M,I lần lượt là trung điểm của CB,CA
=>MI là đường trung bình của ΔBAC
=>MI//AB và \(MI=\dfrac{AB}{2}\)
Ta có: \(MI=\dfrac{AB}{2}\)
\(MI=\dfrac{MK}{2}\)
Do đó: AB=MK
Xét tứ giác ABMK có
MK//AB
MK=AB
Do đó: ABMK là hình bình hành
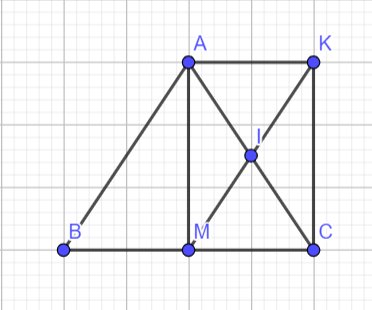
Xét tứ giác AKMC có:
I là trung điểm AC
I là trung điểm MK
`=>` AMCK là hình bình hành
`=>AK=CM` và `AK////CM`
Vì AM là trung tuyến `=>BM=CM`
`=>AK=BM` và `AK////BM`
`=>AKMB` là hình bình hành



