Đáp án C
P = 4 x y 2 x + x 2 + 4 y 2 P = 4 y x 2 1 + 1 + 4 y x 2 3
Đặt 1 + 4 y x 2 = t , t ≥ 1 ⇒ 4 y x 2 = t 2 − 1
Ta được hàm:
f ( t ) = t 2 − 1 1 + t 3 = t − 1 1 + t 2 , t ≥ 1 f ' ( t ) = − t 2 + 2 t + 3 1 + t 4 f ' ( t ) = 0 ⇔ t = − 1 ( L ) t = 3
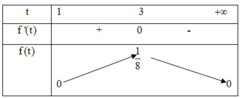
Vậy max P = max [ 1 ; + ∞ ) f ( t ) = 1 8



