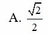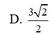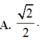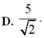Cho các số phức: z, w, u thay đổi thỏa mãn: \(\left|z\right|=\left|w\right|=5\) và: \(\left|z-w\right|^2=8\left|2u-z+w\right|\). Biết rằng: \(\left(z-4i\right)\left(\overline{w}-4i\right)\)và: \(\left(2u+z-w-8i\right)\left(\overline{z-w-2u}\right)\) là số thực dương. Giá trị nhỏ nhất của: \(P=\left|u-2+i\right|+\left|2u+1-3i\right|\)bằng:
\(A.3+\sqrt{2}\) \(B.\sqrt{34}\) \(C.\sqrt{26}\) \(D.3\sqrt{2}+1\)
Đặt: \(\left\{{}\begin{matrix}z=a+bi\\w=c+di\\u=x+yi\end{matrix}\right.\)
\(\left|z-w\right|^2=\left|z\right|^2-2wz+\left|w\right|^2=50-2wz\) \(=50-2ac+2bd-2\left(ad+bc\right)i\) \(\left(1\right)\)
\(8\left|2u-z+w\right|=8\left|2x+2yi-a-bi+c+di\right|=8\sqrt{\left(2x-a+c\right)^2+\left(2y-b+d\right)^2}\)\(=8\sqrt{a^2-2ac-4ax+b^2-2bd-4yb+c^2+4cx+d^2+4dy+4x^2+4y^2}\) \(\left(2\right)\)
\(\left(z-4i\right)\left(\overline{w}-4i\right)=ac-\left(b-4\right)^2+ac\left(d-4\right)i\) biết \(\left\{{}\begin{matrix}ac-\left(b-4\right)^2>0\\ac\left(d-4\right)=0\rightarrow d=4\end{matrix}\right.\)
\(\left(2u+z-w-8i\right)\left(\overline{z-w-2u}\right)=\left(2x+2yi+a+bi-c-di-8i\right)\)\(\left(\overline{a+bi-c-di-2x+2yi}\right)\) \(=a^2-2ac+c^2-4x^2\)\(+(ab+ad-cb-cd-2ya\) \(-2yc+2xb+2xd-4xy)i\) \(+(2ay+ab-ad-8a\) \(-2cy-cb+cd+8c\) \(-4xy-2xb+2xd+16x)i\) \(+2yb-2yd+2y^2+b^2\) \(-bd+2yb-db+d^2+2yd\) \(-8b+8d-16y\) biết phần thực: \(a^2+b^2+c^2+d^2-2ac-2bd-4x^2\)\(+2y^2-8b+8a-16y>0\) và phần ảo: \(2ab-2cb+4cy+4xd\) \(+8xy+8c-8a+16x=0\)
Rút gọn $P$ ta được: \(P=\sqrt{x^2-y^2-4x+5+2i\left(xy-2y\right)}\) \(+\sqrt{2\left(-2x^2+2y^2-6y-2x+4-\left(4xy-2y+3\right)i\right)}\)
\(\rightarrow\) Lú quá đi ngủ!