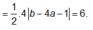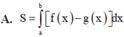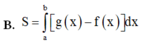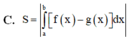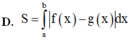Cho các Parabol có các đỉnh lần lượt là I1, I2. Gọi A, B là giao điểm của (P1) và Ox. Biết rằng 4 điểm A, B, I1, I2 tạo thành tứ giác lồi có diện tích bằng 10. Tính diện tích S của tam giác IAB với I là đỉnh của Parabol (P):
y = h(x) = f(x) + g(x). (P1): y = f(x) = 1 4 x 2 - x , P(2): y = g(x) = a x 2 - 4 a x + b (a>0)
A. S = 6.
B. S = 4.
C. S = 9.
D. S = 7.
Chọn A.
(P1): y = f(x) = 1 4 x 2 - x có đỉnh I 2 (2;-1)
P(2): y = g(x) =
a
x
2
-
4
a
x
+
b
(a>0) ![]()
![]()
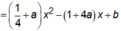
![]()
Duy ra I1, I2, I cùng nằm trên đường thẳng x = 2.
Mà giao điểm của (P1) và Ox là A(4;0) và B(0;0).
Suy ra tứ giác lồi AI1BI2 có hai đường chéo vuông góc và b – 4a >0
![]()
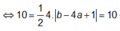
![]()
Tam giác IAB có diện tích là