Các câu hỏi tương tự
Cho hàm số y x3- x2+ x 1 có đồ thị ( C) . Tiếp tuyến tại điểm N( x; y) của (C) cắt đồ thị (C) tại điểm thứ hai là M( -1; -2) . Khi đó x+ y? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho hàm số y= x3- x2+ x= 1 có đồ thị ( C) . Tiếp tuyến tại điểm N( x; y) của (C) cắt đồ thị (C) tại điểm thứ hai là M( -1; -2) . Khi đó x+ y=?
A. 1
B. 2
C. 3
D. 4
Cho hàm số y 2x3-3x2+1 có đồ thị và đường thẳng d: yx-1. Giao điểm của (C) và d lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C là A. BC
30
2
B. BC
34
2
C. BC
3
2
2
D. BC
14
2
Đọc tiếp
Cho hàm số y= 2x3-3x2+1 có đồ thị và đường thẳng d: y=x-1. Giao điểm của (C) và d lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C là
A. BC= 30 2
B. BC= 34 2
C. BC= 3 2 2
D. BC= 14 2
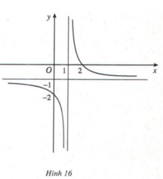
Cho hàm số y = (2 - x)/(x - 1) (H.16) có đồ thị (C).
Nêu nhận xét về khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞
Cho hàm số
y
x
+
2
x
-
2
có đồ thị (C). Xét hình chữ nhật ABCD có
A
B
3
B
C
với A, B, C, D là bốn điểm thuộc đồ thị (C). khi đó độ dài AB bằng
Đọc tiếp
Cho hàm số y = x + 2 x - 2 có đồ thị (C). Xét hình chữ nhật ABCD có A B = 3 B C với A, B, C, D là bốn điểm thuộc đồ thị (C). khi đó độ dài AB bằng
![]()
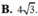
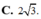
![]()
Cho (C):
x
2
+
(
y
-
2
)
2
1
quay quanh Ox tạo thành khối tròn xoay có thể tích V. Khi đó:
Đọc tiếp
Cho (C): x 2 + ( y - 2 ) 2 = 1 quay quanh Ox tạo thành khối tròn xoay có thể tích V. Khi đó:
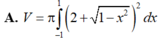
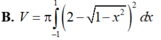
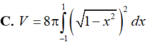
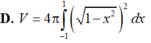
Diện tích hình phẳng giới hạn bởi các đường x-1, x2, y0 và Parabol (P)
y
a
x
2
+
b
x
+
c
bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Khi đó a+b-c bằng bao nhiêu? A. -8 B. -2 C. 14 D. 3
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đường x=-1, x=2, y=0 và Parabol (P) y = a x 2 + b x + c bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Khi đó a+b-c bằng bao nhiêu?
A. -8
B. -2
C. 14
D. 3
Cho hàm số
y
m
x
+
n
x
-
1
có đồ thị (C). Biết tiệm cận ngang của (C) đi qua điểm A(-1; 2) đồng thời điểm I(2; 1) thuộc (C). Khi đó giá trị của m + n là A. m + n -1. B. m + n 1. C. m + n -3. D. m + n 3 .
Đọc tiếp
Cho hàm số y = m x + n x - 1 có đồ thị (C). Biết tiệm cận ngang của (C) đi qua điểm A(-1; 2) đồng thời điểm I(2; 1) thuộc (C). Khi đó giá trị của m + n là
A. m + n = -1.
B. m + n = 1.
C. m + n = -3.
D. m + n = 3 .
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
−
2
1
y
+
1
1
z
+
1
−
2
và
Δ
:
x
−
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x − 2 1 = y + 1 1 = z + 1 − 2 và Δ : x − 3 1 = y + 1 1 = z + 3 2 . Viết phương trình mặt phẳng (P) chứa d và tạo với tam giác một góc 30 ° . có dạng x + a y + b z + c = 0 với a , b , c ∈ ℤ khi đó giá trị a+b+c là
A. 8
B. -8
C. 7
D. -7
Cho hàm số
y
x
3
−
2
x
2
+
2
x
có đồ thị (C). Gọi
x
1
,
x
2
là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến với (C) vuông góc với đường thẳng
y
−
x
+
2018
. Khi đó
x
1...
Đọc tiếp
Cho hàm số y = x 3 − 2 x 2 + 2 x có đồ thị (C). Gọi x 1 , x 2 là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến với (C) vuông góc với đường thẳng y = − x + 2018 . Khi đó x 1 + x 2 bằng
A. 8 3 .
B. 2 3 .
C. 4 3 .
D. 5 3 .

