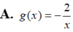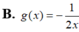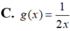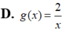Các câu hỏi tương tự
Cho đồ thị (C):
y
x
-
1
x
. Gọi đồ thị (C1): y g(x) là đồ thị đối xứng với (C) qua điểm I(0,1). Xác định g(x).
Đọc tiếp
Cho đồ thị (C): y = x - 1 x . Gọi đồ thị (C1): y = g(x) là đồ thị đối xứng với (C) qua điểm I(0,1). Xác định g(x).
![]()
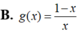
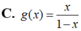
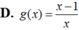
Tọa độ cặp điểm thuộc đồ thị (C) của hàm số y
x
+
4
x
-
2
đối xứng nhau qua đường thẳng d: x-2y-6 0 là A. B. C. D.
Đọc tiếp
Tọa độ cặp điểm thuộc đồ thị (C) của hàm số y = x + 4 x - 2 đối xứng nhau qua đường thẳng d: x-2y-6 = 0 là
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0 Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng (α).
Trong không gian Oxyz, cho mặt phẳng (P): x + y + z - 3 0 và đường thẳng
d
:
x
1
y
+
1
2
z
-
2
-
1
. Đường thẳng d đối xứng với d qua mặt phẳng (P) có phương trình là
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P): x + y + z - 3 = 0 và đường thẳng d : x 1 = y + 1 2 = z - 2 - 1 . Đường thẳng d' đối xứng với d qua mặt phẳng (P) có phương trình là
![]()
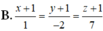
![]()
![]()
Tìm tọa độ A’ đối xứng với A(1,-2,3) qua đường thẳng
d
:
x
-
1
1
y
-
1
z
-
2
1
.
Đọc tiếp
Tìm tọa độ A’ đối xứng với A(1,-2,3) qua đường thẳng d : x - 1 1 = y - 1 = z - 2 1 .
![]()
![]()
![]()
![]()
Cho hàm số y -x3+3mx2-3m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng d: x+8y-740. A. m1 B. m- 2 C. m -1 D. m1
Đọc tiếp
Cho hàm số y= -x3+3mx2-3m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng d: x+8y-74=0.
A. m=1
B. m=- 2
C. m= -1
D. m=1
z = -1 + i được biểu diễn bởi điểm M trong mặt phẳng Oxy. Biết điểm M' biểu diễn số phức w và M’ đối xứng với M qua đường thẳng: ∆ : x-y+1 = 0. Tìm w.
A. w = 0
B. w = 1-i
C. w = 1+i
D. w = -2+2i
Cho hàm số
y
x
-
1
x
+
m
,
m
≠
-
1
, có đồ thị (C). Tìm m để...
Đọc tiếp
Cho hàm số y = x - 1 x + m , m ≠ - 1 , có đồ thị (C). Tìm m để đồ thị (C) nhận I (2;) làm tâm đối xứng.
A. m = 1 2
B. m = - 1 2
C. m = 2
D. m = -2
Cho điểm M(2; -1; 1) và đường thẳng
∆
:
x
-
1
2
y
+
1
-
1
z
2
Tìm tọa...
Đọc tiếp
Cho điểm M(2; -1; 1) và đường thẳng
∆ : x - 1 2 = y + 1 - 1 = z 2
Tìm tọa độ điểm M’ đối xứng với M qua đường thẳng ∆