u → = A D → − C D → + C B → − A B → = ( A D → − A B → ) + ( C B → − C D → ) = B D → + D B → = 0 →
Đáp án B
u → = A D → − C D → + C B → − A B → = ( A D → − A B → ) + ( C B → − C D → ) = B D → + D B → = 0 →
Đáp án B
Đường thẳng d có một vectơ pháp tuyến là n→=(-4,-2). Trong các vectơ sau, vectơ nào là một vectơ chỉ phương của d ?
a. u→=(2,1)
b. u→=(2,4)
c. u→=(-2, 1)
d. u→=(-2, 4)
Trong không gian Oxyz, cho d là đường thẳng đi qua điểm M 0 ( x 0 ; y 0 ; z 0 ) và có vectơ chỉ phương là u → , với a, b, c khác 0. Trong các khẳng định sau, khẳng định nào sai?
A. Phương trình chính tắc của đường thẳng d là: 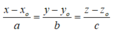
B. Phương trình tham số của đường thẳng d là: x = x 0 + at , y = y 0 + bt , z = z 0 + ct
C. Đường thẳng d nằm trong hai mặt phẳng :(P): b( x - x 0 ) - a ( y - y 0 ) = 0 và (Q): c ( x - x 0 ) - a ( z - z 0 ) = 0
D. Phương trình đường thẳng d là: a ( x - x 0 ) + b ( y - y 0 ) + c ( z - z 0 ) = 0
Cho a+b+c=1.cmr
a)a.b2 .c3 < 1:432
b) b+c > 16abc
c) (1-a)(1-b)(1-c) > 8abc
d)(a+b)(b+c)(a+c)> 8abc
e) a2 (1+b2)+b2(1+c2)+c2(1+a2) > 6abc
Cho bốn điểm phân biệt A, B, C, D. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để A B → = C D → ?
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AC = BD
D. AB = CD
| Câu 11: Trong mặt phẳng Oxy , cho ba vectơ a b c = = - = - (1;2), ( 3;1), ( 4;2) | . Chọn |
. Biết u a b c = + + 3 2 4 khẳng định đúng.
A. u
cùng phương với i
. B. u
không cùng phương với i
.
C. u
cùng phương với j
| . |
D. u
vuông góc với i
Cho tập A = {0; 2; 3; 5} và tập B = {2; 3; 4; 8; 9} và tập C = {2; 5; 7; 8; 10} Khi đó (A n B) U C là tập
A.{2; 3; 8; 9; 10} B.{3; 4; 7; 8; 10} C. {2; 3; 5; 7; 8; 10} D.{2;3;4;5;7;8; 10}Cho 4 điểm phân biệt A, B, C, D. Có bao nhiêu vectơ khác vectơ – không được lập ra từ 4 điểm đã cho?
A. 4
B. 6
C. 12
D. 8
Cho các điểm A, B, C, D, E, F. Khi đó E B → + D E → + A C → + B F → + C D → bằng vectơ nào trong các vectơ sau đây?
A. A E →
B. A F →
C. A D →
D. A C →