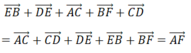Các câu hỏi tương tự
Cho 6 điểm A, B, C, D, E, F. Khẳng định nào sau đây là đúng? A.
A
B
→
+
D
C
→
A
C
→
+
B
D
→
B.
A
B...
Đọc tiếp
Cho 6 điểm A, B, C, D, E, F. Khẳng định nào sau đây là đúng?
A. A B → + D C → = A C → + B D →
B. A B → + B C → = A C → + D B →
C. A D → + B E → + C F → = A E → + B F → + C D →
D. A B → = D C →
Cho tập E = {a,b,c,d} ; F = {b,c,e,g} ; G = {c,d,e,f}
Chứng minh rằng
E giao(F hợp G) = (E giao F) hợp (E giao G)
Trong mặt phẳng Oxy, cho A(-2;0),B(4;0),C(3;5). Gọi D, E, F lần lượt là chân đường cao kẻ từ các đỉnh A, B, C. Tìm tọa độ các điểm E, F và tâm đường tròn nội tiếp tam giác DEF.
Câu 8: Cho hình bình hành ABCD tâm O. Các vectơ khác 0 ngược hướng với OB làA. BD OD , . B. BD OD BO , , . C. DB DO , . D. BD BO , .Câu 9: Cho ba điểm A, B, C thẳng hàng, trong đó điểm B nằm giữa hai điểm A và C. Khi đó các cặp vectơ nào sau đây cùng hướng?A. CB và AB. B. AB và AC. C. AB và CB . D. BA và BC.Câu 10: Cho một đa giác 1 2 2019 A A A ... có 2019 cạnh. Số vectơ khác 0 có điểm đầu và điểm cuối được tạo thành từ các đỉnh của đa giácA. 4074342. B. 8148684. C. 4076361. D. 8152722
Đọc tiếp
Câu 8: Cho hình bình hành ABCD tâm O. Các vectơ khác 0 ngược hướng với OB là
A. BD OD , . B. BD OD BO , , . C. DB DO , . D. BD BO , .
Câu 9: Cho ba điểm A, B, C thẳng hàng, trong đó điểm B nằm giữa hai điểm A và C. Khi đó các cặp vectơ nào sau đây cùng hướng?
A. CB và AB. B. AB và AC. C. AB và CB . D. BA và BC.
Câu 10: Cho một đa giác 1 2 2019 A A A ... có 2019 cạnh. Số vectơ khác 0 có điểm đầu và điểm cuối được tạo thành từ các đỉnh của đa giác
A. 4074342. B. 8148684. C. 4076361. D. 8152722
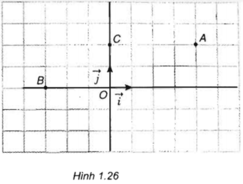
Câu hỏi 3 trang 24: Tìm tọa độ của các điểm A, B, C trong hình 1.26. Cho ba điểm D(-2; 3), E(0; -4), F(3; 0). Hãy vẽ các điểm D, E, F trên mặt phẳng Oxy.
Bài 1:Cho các tập hợp: A={a;b;c;d}, B={a;b}. Hãy tìm tất cả tập X sao cho: B\(\cup\)X=A
Bài 2:A={a,e,i,o}, E={a,b,c,d,i,e,o,f}. Tìm CEA.
Bài 3:Cho: E={x\(\in\)N|x≤8}, A={1,3,5,7}, B={1,2,3,6}. Tìm CEA, CEB, CEA\(\cap\)CEB
Cho hàm số bậc 4 f(x)=\(ax^4+bx^3+cx^2+dx=e\) (\(a\ne0\). Biết rằng các hệ số a,b,c,d,e là các số nguyên không âm và không lớn hơn 8 và f(9)=32078. Tính tổng các hệ số S=a+b+c+d+e
Cho lục giác đều $A B C D E F$ tâm $O$. Chứng minh: $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}+\overrightarrow{O D}+\overrightarrow{O E}+\overrightarrow{O F}=\overrightarrow{0}$.
Cho các tập hợp A {a; b; c; d}; B {b; d; e}; C {a; b; e}. Trong các đẳng thức sau a. A ∩ (B C) (A ∩ B) (A ∩ C). b. A (B ∩ C) (A B) ∩ (A C). c. A ∩ (B C) (A B) ∩ (A C). d. A (B ∩ C) (A B) ∪ (A C). Số đẳng thức sai là A. 1 B. 3 C. 2 D. 4
Đọc tiếp
Cho các tập hợp A = {a; b; c; d}; B = {b; d; e}; C = {a; b; e}. Trong các đẳng thức sau
a. A ∩ (B \ C) = (A ∩ B) \ (A ∩ C).
b. A \ (B ∩ C) = (A \ B) ∩ (A \ C).
c. A ∩ (B \ C) = (A \ B) ∩ (A \ C).
d. A \ (B ∩ C) = (A \ B) ∪ (A \ C).
Số đẳng thức sai là
A. 1
B. 3
C. 2
D. 4