Gọi độ dài của ba đoạn thẳng đã cho là a. Khi đó các đầu mút của chúng là đỉnh của một hình tám mặt đều, mỗi mặt là tam giác đều có cạnh bằng 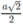
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình bát diện đều ABCDEF.
Chứng minh rằng:
Các đoạn thẳng AF, BD và CE đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.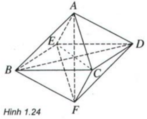
Cho đường tròn (C) tâm O bán kính R và hai đường thẳng d, e cắt mặt phẳng P của đường tròn (C) tại hai điểm A, B là hai đầu mút đường kính của đường tròn ấy. Đường thẳng d vuông góc với mặt phẳng P, d và e chéo nhau. M là một điểm tùy ý của đường tròn (C). Chứng minh rằng tồn tại một và chỉ một đường thẳng delta đi qua M và cắt d, e.
Đọc tiếp
Cho đường tròn (C) tâm O bán kính R và hai đường thẳng d, e cắt mặt phẳng P của đường tròn (C) tại hai điểm A, B là hai đầu mút đường kính của đường tròn ấy. Đường thẳng d vuông góc với mặt phẳng P, d và e chéo nhau. M là một điểm tùy ý của đường tròn (C). Chứng minh rằng tồn tại một và chỉ một đường thẳng delta đi qua M và cắt d, e.
Cho hình chóp S.ABC có SA, SB. SC đôi một vuông góc với nhau và
S
A
1
,
S
B
2
,
S
C
3
. Gọi M là một điểm thuộc miền trong của tam giác ABC sao cho M cách đều các mặt còn lại của hình chóp. Độ dài đoạn thẳng SM bằng
Đọc tiếp
Cho hình chóp S.ABC có SA, SB. SC đôi một vuông góc với nhau và S A = 1 , S B = 2 , S C = 3 . Gọi M là một điểm thuộc miền trong của tam giác ABC sao cho M cách đều các mặt còn lại của hình chóp. Độ dài đoạn thẳng SM bằng
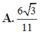
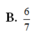
Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau: BA 3a, BC BD 2a. Gọi M và N lần lượt là trung điểm của AB và AD Tính thể tích khối chóp C.BDNM. A.
V
8
a
3
B.
V
2
a
3
3
C.
V
9...
Đọc tiếp
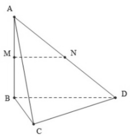
Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau: BA = 3a, BC =BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD Tính thể tích khối chóp C.BDNM.
A. V = 8 a 3
B. V = 2 a 3 3
C. V = 9 a 3 4
D. V = a 3
Cho hai đường thẳng chéo nhau
∆
và
∆
′ có AA’ là đoạn vuông góc chung, trong đó A
∈
∆
và A′
∈
∆
′. Gọi (
α
) là mặt phẳng chứa AA’ và vuông góc với
∆
′ và cho biết AA’ a. Một đường thẳng thay đổi luôn luôn song song với mặt phẳng (
α
) lần lượt cắt
∆
và ...
Đọc tiếp
Cho hai đường thẳng chéo nhau ∆ và ∆ ′ có AA’ là đoạn vuông góc chung, trong đó A ∈ ∆ và A′ ∈ ∆ ′. Gọi ( α ) là mặt phẳng chứa AA’ và vuông góc với ∆ ′ và cho biết AA’ = a. Một đường thẳng thay đổi luôn luôn song song với mặt phẳng ( α ) lần lượt cắt ∆ và ∆ ′ tại M và M’ . Hình chiếu vuông góc của M trên mặt phẳng ( α ) là M 1 . Chứng minh rằng khi x thay đổi mặt cầu tâm O luôn luôn chứa một đường tròn cố định.
II. Tự luận ( 5 điểm)
Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau:
BA = 3a, BC = BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng A.
90
0
B.
30
0
C.
60
0
D.
45
0
Đọc tiếp
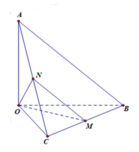
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
A. 90 0
B. 30 0
C. 60 0
D. 45 0
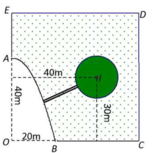
Một cái ao có hình ABCDE (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 10m, người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hỏi độ dài ngắn nhất l của cây cầu gần nhất với so nào dưới đây biết. - Hai bờ AE và BC nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại điểm O; - Bờ AB là một phần của một parabol có đỉnh là điểm A và có trục đối xứng là đường thẳng OA ; - Độ dài đoạn OA và OB lần lượt là 40m và 20m; - Tâm I của mảnh vườn cách đường thẳn...
Đọc tiếp
Một cái ao có hình ABCDE (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 10m, người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hỏi độ dài ngắn nhất l của cây cầu gần nhất với so nào dưới đây biết.
- Hai bờ AE và BC nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại điểm O;
- Bờ AB là một phần của một parabol có đỉnh là điểm A và có trục đối xứng là đường thẳng OA ;
- Độ dài đoạn OA và OB lần lượt là 40m và 20m;
- Tâm I của mảnh vườn cách đường thẳng AE và BC lần lượt là 40m và 30m.
A. 29,7m
B. 17,7m
C. 11,7m
D. 6,7m
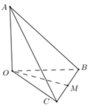
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA OB OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng A.
90
o
B.
30
o
C.
60
o
D.
45
o
Đọc tiếp
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA =OB= OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
A. 90 o
B. 30 o
C. 60 o
D. 45 o

