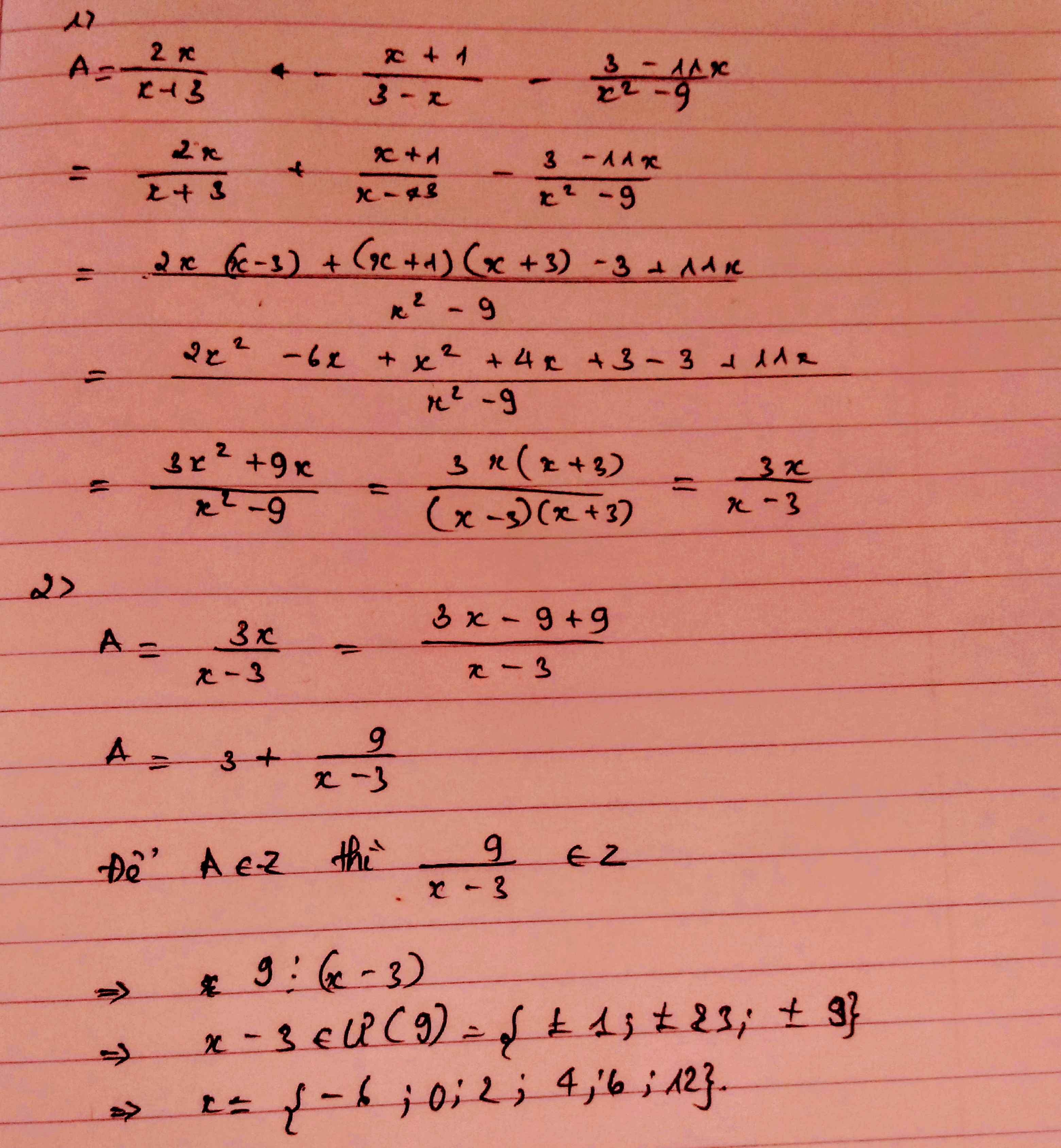Question

cho \(A=\dfrac{2x}{x+3}-\dfrac{x+1}{3-x}-\dfrac{3-11x}{x^2-9}\) ĐK: `x ≠+-3`

1. Rút gọn A

2. Tìm \(x \in Z\) để \(A \in Z\)

Answer 1

Answer 2

`1,` Với `x \ne +-3` có:

`A=[2x]/[x+3]-[x+1]/[3-x]-[3-11x]/[x^2-9]`

`A=[2x(x-3)+(x+1)(x+3)-3+11x]/[(x-3)(x+3)]`

`A=[2x^2-6x+x^2+3x+x+3-3+11x]/[(x-3)(x+3)]`

`A=[3x^2+9x]/[(x-3)(x+3)]`

`A=[3x(x+3)]/[(x-3)(x+3)]=[3x]/[x-3]`

`2,` Với `x \ne +-3` có:

`A=[3x]/[x-3]=[3x-9+9]/[x-3]=[3(x-3)+9]/[x-3]=3+9/[x-3]`

 Để `A in ZZ<=>3+9/[x-3] in ZZ`

           `=>9/[x-3] in ZZ`

  `=>x-3 in Ư_9`

Mà `Ư_9={+-1;+-3;+-9}`

\begin{array}{|c|c|c|}\hline x-3&-1&1&-3&3&-9&9\\\hline x&2&4&0&6&-6&12 \\\hline\end{array}

Mà `x in ZZ,x \ne +-3=>x in {2;4;0;6;-6;12}`

 

 

 

Answer 3