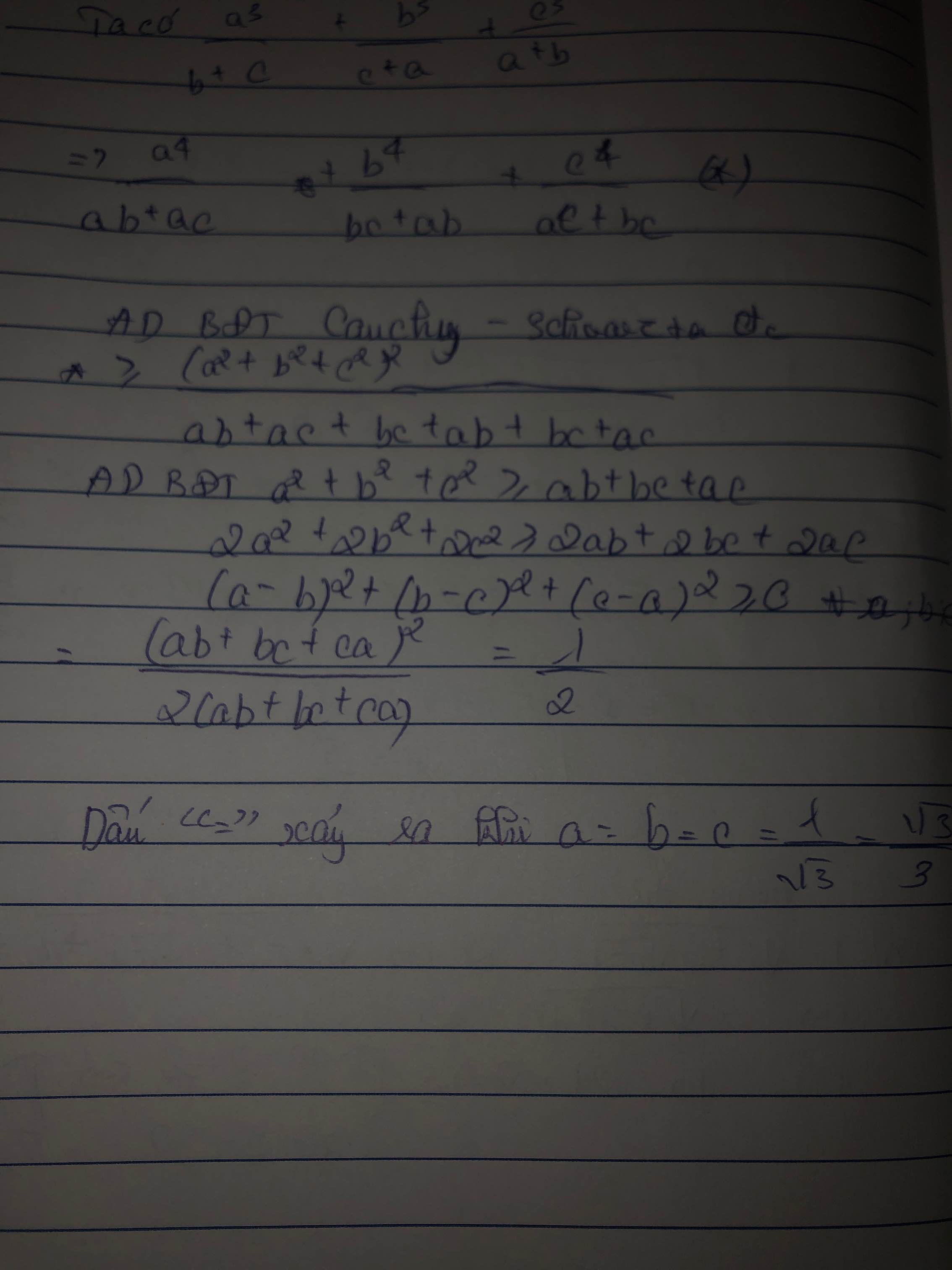Đặt vế trái BĐT là P
Ta có:
\(\left(\dfrac{a^3}{b+c}+\dfrac{b^3}{c+a}+\dfrac{c^3}{a+b}\right)\left(a\left(b+c\right)+b\left(c+a\right)+c\left(a+b\right)\right)\ge\left(a^2+b^2+c^2\right)^2\)
\(\Rightarrow P.\left(2ab+2bc+2ca\right)\ge1\)
\(\Rightarrow P\ge\dfrac{1}{2\left(ab+bc+ca\right)}\ge\dfrac{1}{2\left(a^2+b^2+c^2\right)}=\dfrac{1}{2}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{\sqrt{3}}\)