Áp dụng định lý Pytago trong tam giác vuông: ABC :
![]()
Áp dụng hệ thức lượng trong tam giác vuông ABC:
![]()
M là trung điểm củaBC
![]()
Vậy HM = BM – BH = 7 10 (cm)
Đáp án cần chọn là: A

Áp dụng định lý Pytago trong tam giác vuông: ABC :
![]()
Áp dụng hệ thức lượng trong tam giác vuông ABC:
![]()
M là trung điểm củaBC
![]()
Vậy HM = BM – BH = 7 10 (cm)
Đáp án cần chọn là: A
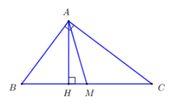
Cho tam giác ABC có độ dài các cạnh AB , BC ,AC ( theo đơn vị cm ) là ba số tự nhiên liên tiếp tăng dần có đường cao AH , đường trung tuyến AM. Tính độ dài đoạn thẳng HM ( theo đơn vị cm )
Tam giác ABC vuông tại A,có AB=3cm,AC=4cm, đường cao AH, trung tuyến AM.tính độ dài HM
Tam giác ABC vuông tại A,có AB=3cm,AC=4cm, đường cao AH, trung tuyến AM.tính độ dài HM
Tam giác ABC vuông tại A,có AB=3cm,AC=4cm, đường cao AH, trung tuyến AM.tính độ dài HM
Bài 4. Cho tam giác ABC vuông tại A có AB AC , đường cao AH , trung
tuyến AM .
a) (cả hình) Giả sử BH cm;CH cm = = 18 32 . Tính độ dài đoạn thẳng HM .
b) Gọi E và F lần lượt là hình chiếu của điểm H trên cạnh AB và AC . AM
cắt FE tại K . Chứng minh FE vuông góc với AM
Cho tam giác ABC vuông tại A đường cao AH
a) AB=12cm,BC=20cm.Tính AC, AH, góc ABC(làm tròn đến độ)
B) kẻ HM vuông góc AB tại M, HN vuông góc AC tại N. CM: AN. NC=AC^2 -HC^2
c) CM: AH= MN, CM: AM. MB+AN. NC=AH^2
Cho ∆ABC vuông tại A, đường cao AH. Bt AB = 12cm, BC = 20cm.
a) Tính AH, AC, góc ABC.
b) Kẻ HM⊥AB tại M, HN⊥AC tại N. Cm AN × AC = AC² - HC²
c) Cm AH = MN; AM × MB + AN × NC = AH²
d) Cm tan³C = BM/CN
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HM ⊥ AB;HN ⊥ AC. Biết AB = 3cm; AC = 4 cm
c) Tính diện tích tứ giác BMNC
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HM ⊥ AB;HN ⊥ AC. Biết AB = 3cm; AC = 4 cm
a) Tính BC, BH, CH, MN