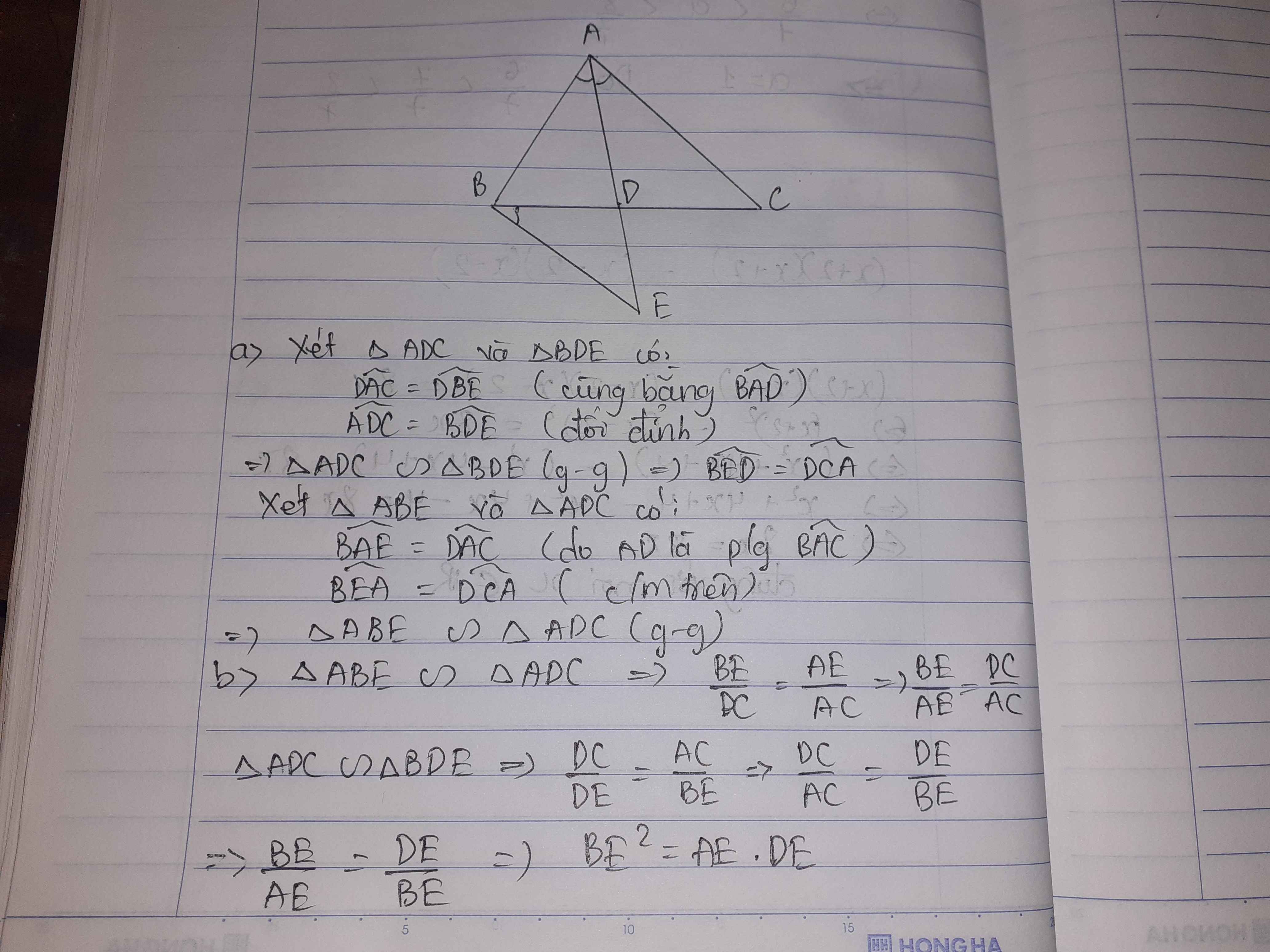
a) Xét ΔABE và ΔADC có
\(\widehat{BAE}=\widehat{DAC}\)(hai góc đối đỉnh)
\(\widehat{AEB}=\widehat{ACD}\)(ΔDBE\(\sim\)ΔDAC)
Do đó: ΔABE\(\sim\)ΔADC(g-g)
b) Xét ΔEBD và ΔEAB có
\(\widehat{BEA}\) chung
\(\widehat{EBD}=\widehat{EAB}\)(gt)
Do đó: ΔEBD\(\sim\)ΔEAB(g-g)
Suy ra: \(\dfrac{BE}{AE}=\dfrac{DE}{BE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(BE^2=DE\cdot AE\)