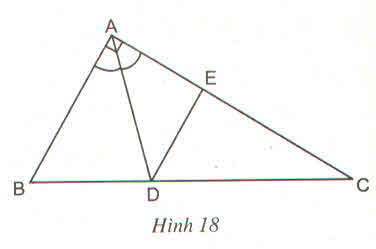
1. Cho △ABC có AB6cm,AC9cm,BC7,5cm. Đường phân giác trong và ngoài của  cắt BC lần lượt ở D và E. Tính BD, BE, ED ?
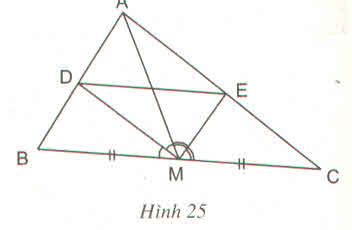
2. Cho △ABC, trung tuyến AM. Đường phân giác của widehat{AMB} cắt AB ở D, đường phân giác của widehat{AMC} cắt AC ở E. Gọi I là giao điểm của IE và AM.
a) CMR: DE//BC
b) CMR: I là trung điểm của DE
3. Cho △ABC vuông ở A, biết AB20cm,AC21cm
a) Tính BC?
b) Đường phân giác của  cắt BC ở D. Tính DB, DC?
c) Qua D kẻ đường thẳng // AC cắt AB tại E. Qua D kẻ đường thẳng // AB cắt...
Đọc tiếp
1. Cho △ABC có \(AB=6cm,AC=9cm,BC=7,5cm\). Đường phân giác trong và ngoài của  cắt BC lần lượt ở D và E. Tính BD, BE, ED ?
2. Cho △ABC, trung tuyến AM. Đường phân giác của \(\widehat{AMB}\) cắt AB ở D, đường phân giác của \(\widehat{AMC}\) cắt AC ở E. Gọi I là giao điểm của IE và AM.
a) CMR: DE//BC
b) CMR: I là trung điểm của DE
3. Cho △ABC vuông ở A, biết \(AB=20cm,AC=21cm\)
a) Tính BC?
b) Đường phân giác của  cắt BC ở D. Tính DB, DC?
c) Qua D kẻ đường thẳng // AC cắt AB tại E. Qua D kẻ đường thẳng // AB cắt AC tại F. Tứ giác AEDF là hình gì? Tính diện tích của tứ giác đó.
4. Cho △ABC có chu vi 27cm, BC là cạnh lớn nhất của △. Đường phân giác của \(\widehat{C}\) chia AB thành 2 đoạn tỉ lệ với \(\frac{1}{2}\). Đường phân giác của \(\widehat{C}\) chia AB thành 2 đoạn tỉ lệ với \(\frac{3}{4}\). Tính độ dài các cạnh của △ABC.
*Lưu ý: Có vẽ hình và khi chứng minh cần có dấu hiệu trong( ... ). Vd: tam giác ABC cân ⇒ AB=AC (tính chất tam giác cân)