Question

Cho △ABC có AB = AC. Đường thẳng qua B vuông góc với AB cắt đường thẳng qua C vuông góc với AC tại O. Chứng minh:

a) △ABO = △ACO.

b) AO ⊥ BC.

c) Góc BCO = Góc CBO.

Answer 1

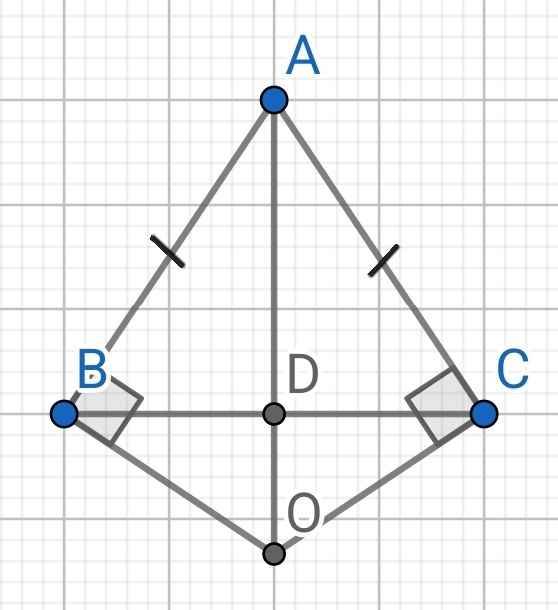
 a) Xét hai tam giác vuông: ∆ABO và ∆ACO có:

AO là cạnh chung

AB = AC (gt)

⇒ ∆ABO = ∆ACO (cạnh huyền - cạnh góc vuông)

b) Gọi D là giao điểm của AO và BC

Do ∆ABO = ∆ACO (cmt)

⇒ ∠BAO = ∠CAO (hai góc tương ứng)

⇒ ∠BAD = ∠CAD

Xét ∆ABD và ∆ACD có:

AD là cạnh chung

∠BAD = ∠CAD (cmt)

AB = AC (gt)

⇒ ∆ABD = ∆ACD (c-g-c)

⇒ ∠ADB = ∠ADC (hai góc tương ứng)

Mà ∠ADB + ∠ADC = 180⁰ (kề bù)

⇒ ∠ADB = ∠ADC = 180⁰ : 2

= 90⁰

⇒ AD ⊥ BC

⇒ AO ⊥ BC

c) ∆ABO = ∆ACO (cmt)

⇒ BO = CO (hai cạnh tương ứng)

Do ∆ABD = ∆ACD (cmt)

⇒ BD = CD (hai cạnh tương ứng)

Xét ∆BOD và ∆COD có:

BO = CO (cmt)

BD = CD (cmt)

OD là cạnh chung

⇒ ∆BOD = ∆COD (c-c-c)

⇒ ∠OBD = ∠OCD (hai góc tương ứng)

⇒ ∠OBC = ∠OCB

Vậy ∠BCO = ∠CBO